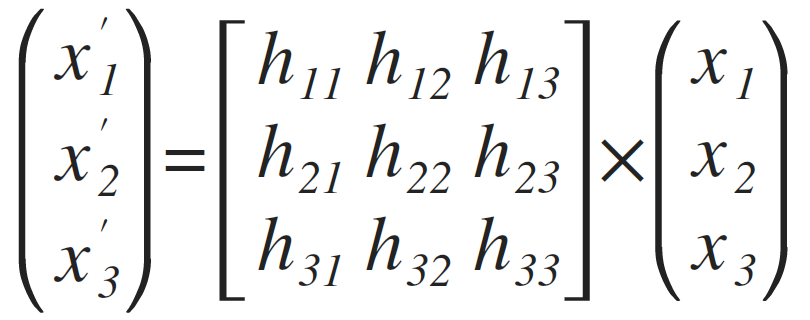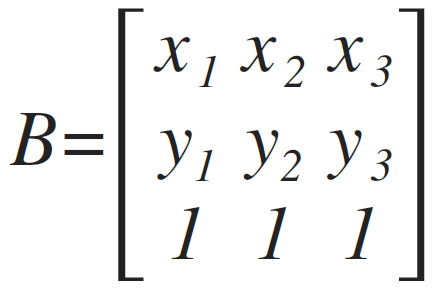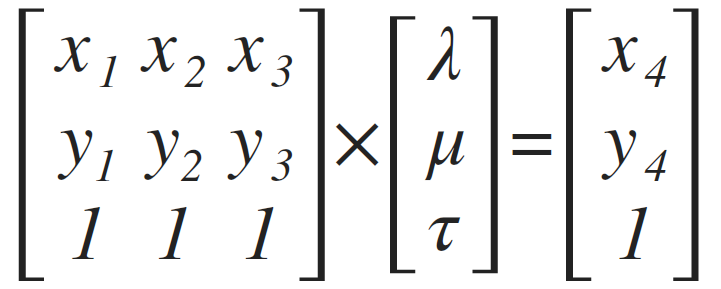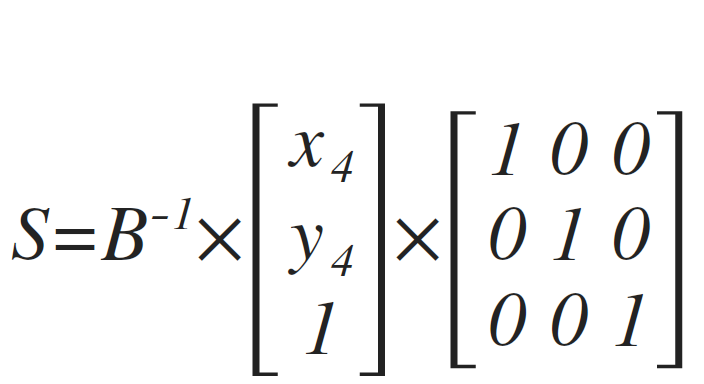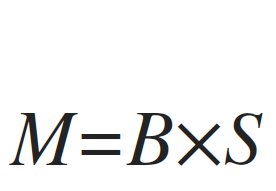Matrix Math

Perspective Transform is Homography Matrix

SIMD Framework

Using Apple built-in Swift SIMD Framework. See more on Single Instruction Multiple Data (SIMD).

We can take advantage of the matrix calculations that framework offers. To calculate transformation we perform one multiplication and one inverse operations. SIMD can parallelize execution of those operations on multiple CPU cores. Result matrix can be calculated as fast as single devision and multiplication.

Homography Matrix

By definition H is homography matrix when x' = H x

For а set of basis vectors, we can represent H as:

H = M(x')/M(x) = M' * M⁻¹

Then all we have to do is to find M that transforms perspective to base vectors coordinates.

Matrix calculation

Determine a homography H given 4 point correspondences. One way to express M matrix is in terms of base vectors:

(1,0,0)
(0,1,0)
(0,0,1)
(1,1,1)

For given 4 points we can define base vector based on first 3 points:

And scale them so that 4th points maps to (1,1,1) point:

Then one of the solutions can be calculated as:

giving us M as