-
Notifications
You must be signed in to change notification settings - Fork 0
Internship Report
本次iLab暑期实习的第一天,实验室研究生学长认真负责的为我们讲解了本次暑期实习的计划安排和流程,在明白了我们假期大致要做什么事情之后就开始了第一周的理论知识学习。
听到深度学习、人工智能这些名词早就不是一天两天了,但是真的进入这个世界的大门确的的确确是这个暑假在ilab的实习。第一周的深度学习理论知识学习让我了解到、接触到、过渡到人工智能方面的研究,这也为我下学期专业课打下了一个比较坚实的基础。
在第一周的理论学习中,我主要是分以下两方面进行研究学习:
- 7.20~7.25分别阅读《吴恩达深度学习课程笔记》前几章章节,并每日将所学知识整理成笔记
- 7.20日作为接触深度学习的第一天,主要了解了深度学习能做的事什么?能处理的是什么问题;接着明白了这一整套课的学习目标;什么是神经网络?在这一章节中老师以一个小例子作为引例,生动而又形象的描述了深度学习与日常生活的关联,也更坚定了我想学好深度学习的决心;接下来明白了深度学习的分类以及如何在不同的应用领域选择合适的神经网络,如何根据数据类型的不同准确使用对应的深度神经网络解决问题;最后详细的阅读了老师对本门课的要求,也让我更加严格的对待自己,对待这门课。
- 7.21日开始正式接触深度神经网络,首先的不是编写代码,而是把编写代码之前的理论知识打牢打扎实,学习了二分类及其符号定义;逻辑回归中的假设函数(尤其是sigmoid函数);逻辑回归的代价函数和损失函数;以及梯度下降法。
- 7.22日接着学习编程基础的后续内容,包括在编程的角度重新审视导数及其含义;掌握了一个全新的概念---计算图,主要从计算图的代价函数计算,计算图的导数计算两方面了解并使用计算图;接着在上节课的梯度下降法的基础上了解函数回归中的梯度下降。
- 7.23日是神经网络编程基础的收尾阶段,将传统的循环方法转化为向量化的思想;并用向量法重新审视逻辑回归(主要包括前向传播的向量化,梯度下降的向量化,逻辑回归的向量化);之后从python编程的实例上了解广播的定义以及它的使用方法,并了解了广播的优缺点;最后一个比较重要的知识点就是一维数组与向量的不同点,如果不是老师再三强调,在最后的项目中肯定会弄混这两个结构和造成莫名其妙的bug。
- 7.24日在学习完深度神经网络的编程基础后开始决定实战,于是安装了Jupyter Notebook,并且分别在Windows系统和MacOS系统中都成功安装Jutyper Norebook,同时也写了第一个myfirst.ipynb笔记,充分了解了它的使用。
- 7.25日进入浅层神经网络的学习,由于有很多概念不是很清楚,所以这一个章节的学习速率较慢,主要是希望把基础打牢,主要学习了神经网络的表示;如何计算神经网络的输出。
- 7.25 进行第一周测验和第二周测验,验收所学知识的掌握程度
- 第一周测验主要是对《深度学习简介》内容的检验,共有10道题,做对9道题,做错一道多选题,知识点主要疏漏在对机器学习处理数据类型不同时采用的策略也不同一知识点上:在循环神经网络应用机器翻译将英语翻译成法语的过程中可行的原因是RNN可被用做监督学习,并且比较适合用于当输入/输出是一个序列的时候;并且RNNs代表递归的过程不是:想法-编码-实验-想法-...
- 第二周测验主要是对《神经网络基础》内容的检查,前5题中全部做对,并且在编程题中给出了不止一种解法。
主要围绕5种典型的网络结构进行调研,在网上和书上阅读并整理了各个网络结构的基本内容,包括基本架构,模型本身,以及对应模型的Keras实现等
网络模型包括:
- LeNet
- AlexNet
- Googlenet
- VGG
- Resent
在5种典型网络的学习中让我明白了软件开发或者具体点说是深度学习中模型的优化的过程,以及每个团队在前人基础上进行的创新和再实践,这也启发我要站在前人的肩膀上思考问题并解决问题,才能站得更高、看得更远,并最终有所成就;在深度学习的模型建立上也是一样,要多参考前人优秀的模型,并深刻理解前人如此创建模型的意义,将其核心思想提炼出来并加以总结,这样在今后同类型问题,或者有相似结构问题的求解中会起到大用处,不仅可以节省我们训练模型的成本,更可以让我们的模型有更好的性能和效果。
第三部分主要是在理论知识大致掌握之后进行的实战项目,也是深度学习的经典入门案例,虽然是比较简单的MNIST数据集上的手写数字的识别,虽然是比较初级,但是选择这个数据集作为入门有几方面的好处:
- 作为经典数据集网上有很多教程以及详细的讲解
- 使用初级数据集作为入门,可以暂且忽略掉一些高级的技术,而是把注意力放在如何从分析问题开始一步步搭建深度神经网络并最终完成测试数据集的测试
- 可以充分理解整个训练深度神经网络的流程以及各种不同的神经网络的工作过程
- 分别使用多层神经网络和卷积神经网络对MNIST数据集进行训练,可以比较二者的思想的相同点和不同点,以及比价二者的效果。为以后提炼二者的思想精髓进而创造出更好的深度神经网络而做铺垫。
建立于2014年,团队成员包括路建伟教授,刘博教授级高级工程师、罗烨助理教授、于天维教授、刑毅教授、郝柯教授,以及6名博士生和23名硕士生。依据人工智能算法,立足解决计算机视觉、智能机器人、医学图像诊断等领域方向的科研以及实际问题。
-
智能机器人
感知上带有激光指示、自主导航、绘制地图、自动避障、气体检测、噪声监测、照度检测等;交互上带有语音识别、语义理解、语音合成、人脸识别,带有RFID、二维码识别、智能设备等;运动控制上带有可移动底盘、机械手臂、机械颈部、腰部等;人工智能方面带有自有知识库、深度学习框架、自主地图构建导航、自主充电等。
技术研究优势有"基于深度学习的双目立体视觉算法"、"基于视觉显著性的图像描述+场景定位"、知识库的自助学习算法、多维度的疾病模型等
-
医学图像
使用人工智能算法,利用可变的深度学习网络结构,提供高于世界先进水平的诊断结果,包括良恶性、钙化级别等,软件性能、数据处理流程能满足临床应用需求和国家相关标准被要求。
现主要应用于智能医学图像辅助诊断系统,有肺结节良恶性诊断、乳腺癌早期诊断和基于眼底图像的糖网病检测诊断三个方面。
肺结节智能诊断通过深度学习相关算法实现对CT图像肺结节自动诊断,针对小于5mm的结节以及病人的随访历史医学影像数据进行未来病症的预测,良恶性分裂准确率已达90.1%。乳腺癌早期诊断通过深度学习相关算法对多种模态的乳腺影像数据建模,实现乳腺癌的检测和早期良恶性诊断,并区别由于女性生理期导致的炎症等假性病症,从而提高识别准确度。眼底图像的糖网病检测通过输入的眼底彩色图像,对当前病人的糖尿病程度进行评分并生成对应血管树,医生再初筛结果中严重病变的病人进行重点诊疗。
-
智慧医疗
结合大数据和人工智能的医疗系统,结合多维度的疾病知识库,为患者提供诊前、诊中及诊后全方位服务。
依托智能导诊机器人,依据多维度疾病模型,通过语音和触摸屏与患者人机交互,引导患者了解病情,给出就诊科室建议,实现自助分诊。同时设计就医服务,为患者提供医生排班、停诊须知、就医流程、就诊须知、药品查询、检查项目查询等辅助就医服务。建立多维度疾病模型数据库,通过对医疗大数据挖掘分析,为8000多种常见疾病,构建了典型症状、发病原因、预防、临床检查、鉴别、治疗方法、护理、饮食保健、并发症等九个分析维度。
- 网络搜索和广告
- 读取X光图像
- 个性化教育
- 精准化农业
- 智能驾驶......
- 建立神经网络(包含深度神经网络)
- 在数据上训练他们
- 用深度神经网络辨认猫
- 严密的构建神经网络
- 如何让他表现更好(超参数调整, 正则化, 诊断偏差, 方差, 高级优化算法[Momentum, Adam算法)
- 结构化机器学习工程
- 端对端深度学习
- 热门领域的建立并且改良许多深度学习问题
- 卷积神经网络(CNN(s)) --> 图像领域
- 序列模型 --> 自然语言处理(NLP)
- 循环神经网络(RNN)
- 长短期记忆网络(LSTM)
*(个人理解)*首先找到一些输入变量(即哪些因素会影响到最终你将预测的东西), 多个输入之间会进一步影响某些共同的中间节点, 而这些中间节点又共同影响最终将预测的输出
第0层的初始输入可能影响到第1层, 第2层, 第i层的中间节点; 第1层的中间节点同样会影响到第2层, 第3层,第i层的节点, 以此类推...
类似于人类大脑中的神经元, 一个神经元不是孤立存在的, 前端的神经元会与后端的神经元有千丝万缕的联系, 而这些联系不断丰富不断扩张就构成了庞大的神经网络; 最终我们应用这个神经网络就可以完成我们从输入-->输出的预测了
房价预测的例子:
通过房屋的面积 --预测--> 房价
初始解决方案: 线性回归, 并且关注到房价永远非负, 因此当房屋面积很小时, 房价为0
神经网络:
- 输入: 房屋的面积 x
- 输出: 价格 y
- 神经元: 中间节点
模型: ReLU激活函数 (rectify <=> max(0,x)
扩展: 现在不止面积会影响房价, 房间数量, 邮编, 富裕程度都会影响房屋的价格; 那么现在x就是这四个输入, y是预测的价格; 把这些单个的神经元叠加在一起就有了一个稍微大一点的神经网络
-
数据库中的结构化数据(广告, 房地产等) ---> 标准的神经网络
-
图像 ---> 卷积CNN
-
序列数据(如音频, 有时间组件) ---> 递归神经网络RNN
-
自然语言 ---> RNNs
- 结构化数据: 数据中的基本数据
- 非结构化数据: 音频/图像/文本
人类更善于理解非结构化数据, 而计算机更擅长处理结构化数据
- 更大的神经网络
- 更多的数据: 近十年数字化社会的额来临, 数据量变得非常大, 远超过机器学习算法能够高效发挥优势的规模
- 但最终耗尽了数据, 或者最终网络规模太巨大以至于要用太久的时间去训练, 都会成为深度学习表现的瓶颈
- 如果没有大量的训练集, 最终的效果会取决于特征工程能力
- 在数据集不多的时候, 效果取决于工程选择特征方面的能力以及算法的不同
- 只有当数据规模非常庞大的时候, 更大的神经网络的效果更好
- 之前的机器学习主要局限于训练一个特大神经网络耗费的时间和资源上
凭直觉观察到特征:arrow_right:写代码实现想法:arrow_right:...实验:arrow_right:参考神经网络的效果修改细节:arrow_right:再次实验...
- 如何处理训练集 --> 打破习惯的for循环遍历训练集的每个样本
- 神经网络训练过程: 前向暂停, 前向传播 --> 反向暂停, 反向传播
- 逻辑回归
引例: 一张彩色图片是不是猫?
输入: 一张图片, 也就是三个64*64的矩阵
输出: 结果标签(0或1), 用于表示是否为猫
我们再定义一个nx表示输入特征向量的维度, 这里我们采用的规则是把rgb三个矩阵中的每一个数值都一次排列, 最终形成的是一个64 * 64 * 3的一维向量, 构成我们的额特征向量x; 我们构建的神经网络就是通过这个12288维的向量作为输入, 输出0或1, 也就是预测图片中是否有猫
-
x: 输入数据, 维度是 nx * 1
-
y: 输出结果, 取值是(0, 1)
-
X = [x(1), x(2), ... , x(m)]: 所有训练数据集的输入值, 维度是 nx * m
(如果X中的项是按行给出的, 我们可以对其转置, 神经网络中一般采用👇这种形式)
-
Y = [y(1), y(2), ... , y(m)]: 所有训练数据集的输出值, 维度是 1 * m
-
(x(i), y(i)): 第i个单独的样本(输入/输出)
-
Mtrain: 训练样本的个数
-
Mtest: 测试集的样本数
ps. 可以通过X.shape获取X矩阵的规模(nx, m), Y.shape获取Y矩阵的规模(1, m)
-
$\hat{y}$ 表示y等于1的一种可能性, 也就是对实际值y的估计 - w表示逻辑回归的参数, 特征权重, 维度为nx, 与特征向量相同
- b表示偏差, 是一个实数
如果令 sigmoid函数, 将线性函数转换为非线性函数
- 值域平滑的从0走到1
- 纵轴的截距是0.5
目标是让机器学习参数w和b使的$\hat{y}$成为y=1这一情况概率的一个很好的估计
通过训练代价函数可以得到参数w和参数b => 进而训练逻辑回归模型
L(
一般使用与测试和实际值的平方差或者平方差的一半, 但是由于我们的优化目标不是凸优化, 只能找到多个局部最优值
L(
我们希望逻辑回归损失函数尽可能小:
- 当y=1时, 损失函数L(
$\hat{y}$ , y) = -ylog($\hat{y}$ ), 当L尽可能小时,$\hat{y}$ 就要尽可能大, 因为sigmoid函数的取值范围时[0,1], 因此$\hat{y}$无限接近于1, 与y很接近 - 当y=0时, 损失函数L(
$\hat{y}$ , y) = -log(1 -$\hat{y}$ ), 当L尽可能小时,$\hat{y}$ 就要尽可能小, 因为sigmoid函数的取值范围时[0,1], 因此$\hat{y}$无限接近于0, 与y很接近 - 这门课中有很多函数: 如果y等于1, 就要让$\hat{y}$尽可能大; 如果y等于0, 就要让$\hat{y}$尽可能小
对m个样本的损失函数求和然后除以m, 我们要找到合适的w和b让代价函数J的总代价降到最低
通过最小化代价函数J(w, b)来训练参数w和b
形象化J为
代价函数J(w,b)是在水平轴w和b上的曲面, 曲面的高度就是J(w,b)在某点的函数值
- 首先采用随机初始化方法在曲面上随机取一点, 初始化参数w和b(因为函数为凸函数, 因此无论在哪里初始化最终结果大致相同)
- 朝嘴都的下坡方向走一步, 不断迭代
- 知道走到全局最优解或者接近全局最优解的地方
暂且忽略参数b, 只考虑一维的w
-
$\alpha$ 表示学习率, 用来控制补偿 -
$\frac{d J(w)}{d w}$ 是函数J(w)对w求导 -
当随机点位于最小值右侧时, 斜率(导数)大于零, 每次w减小一点, 往左移一点, 直到到达最低点
-
当随机点位于最小值左侧时, 斜率(导数)小于零, 每次w增大一点, 往右移一点, 直到到达最低点
考虑w和b两个参数
在f(a) = 3a例子中, 无论当a=2还是a=5时, a向右偏移0.001使得f(a)增加的量比上a增加的量都是3
更直观的来看是该直线的斜率是3, 也就是小三角形的高/宽是3
f(a)增大的值为点在a处的斜率或导数, 乘以向右移动的距离
(这里需要注意, 导数增大的值, 不是等于的导数公式算出来的值, 二十根据导数算出来的一个估计值)
例f(a) = a3 f'(a) = 3a2, 令a=2, 则a3=8, 如果a增大0.001, f'(2)=12, 所以f(a)变大12*0.001 = 0.012, f(a)=8.012 这和真实的2.0013十分接近
一个神经网络的计算, 都是按照前向或反向传播过程组织的
- 首先计算出一个新的网络的输出(前向过程)
- 紧接着进行一个反向传输操作 --> 用来计算出对应的梯度或导数
例如, 函数为3(a + bc), 计算步骤为
- 计算b*c, 把它储存在u中
- 计算v=a+u
- 最后输出J=3v
(蓝线从左到右是计算代价函数J的步骤, 红线从右到左是计算导数的方式)
详细解释下$\frac{d J}{d a} $的计算:
例子中a=5, 我们让它编程概念5.001, 那么对v的影响就是a+u, 之前v=11, 现在变成11.001, J因此变成33.003
当a增加0.001, J增加0.003, 因此$\frac{d J}{d a} $=3
(如果改变a, 那么也会改变v, 如果改变v, 也会改变J, 所以J的净变化量就是当把a提高0.001时变化的0.003)
-
dvar: 表示输出变量对变量var的导数, 是$\frac{d FinalOutputvar}{d var} $ --> dFinalOutputvar_dvar的简写
例如上面的$\frac{d J}{d a} $ 用变量da表示
损失函数:
代价函数:
梯度下降法:
- w的修正值:
$W :=W-a \frac{\partial J(w, b)}{\partial w}$ - b的修正值:
$b :=b-a \frac{\partial J(w, b)}{\partial b}$
假设只有两个特征x1和x2, 为了计算z, 我们需要输入参数w1, w2和b
单个样本的代价函数为$L(a, y)=-(y \log (a)+(1-y) \log (1-a))$, a是逻辑回归的输出, y是样本的标签值
结果:
- da:
$\frac{d L(a, y)}{d a}=-y / a+(1-y) /(1-a)$ - dz:$\frac{d L(a, y)}{d z}=\frac{d L}{d z}=\left(\frac{d L}{d a}\right) \cdot\left(\frac{d a}{d z}\right)=\left(-\frac{y}{a}+\frac{(1-y)}{(1-a)}\right) \cdot a(1-a)=a-y$
- dw1:$\frac{1}{m} \sum_{i}^{m} x_{1}^{(i)}\left(a^{(i)}-y^{(i)}\right)$
- dw2:
$\frac{1}{m} \sum_{i}^{m} x_{2}^{(i)}\left(a^{(i)}-y^{(i)}\right)$ - db:
$\frac{1}{m} \sum_{i}^{m}\left(a^{(i)}-y^{(i)}\right)$
- 计算dz: dz = (a - y)
- 计算dw1: dw1 = x1 * dz
- 计算dw2: dw2 = x2 * dz
- 计算db: db = dz
- 更新w1: w1 = w1 - a * dw1
- 更新w2: w2 = w2 - a * dw2
- 更新b: b = b - a * db
J,dw1,dw2,db = 0,0,0,0
for i in range(0,m):
z[i] = w*x[i] + b
a[i] = sigmoid(z[i])
J += -(y[i]*log(a[i]) + (1-y[i])*log(1-a[i]))
dz[i] = a[i] - y[i]
dw1 += x1[i] * dz[i]
dw2 += x2[i] * dz[i]
db += dz[i]
J /= m
dw1 /= m
dw2 /= m
db /=m
w -= alpha * dw
b -= alpha * db- 算法中不要显示的使用for循环 --> 向量技术 (为了适应越来越大的数据集)
例1. 计算$z=w^{T} x+b$
import numpy as np
# 暴力循环法
def forloop(w,x,b):
z = 0
for i in range(len(x)):
z += w[i]*x[i]
z += b
# 向量法
def vector(w,x,b):
z = np.dot(w,x) + b
if __name__ == "__main__":
w = [w for w in range(1,1000)]
x = [x for x in range(1000,1,-1)]
b = 100
forloop(w,x,b)
vector(w,x,b)但实际测试过后, 将每种算法执行5000次, 运行结果如下:
Time forloop: 5.08 Time vector: 7.18
但是如果将产生数组的方式更换为
w = np.random.rand(1000000)
x = np.random.rand(1000000)向量化的版本运行效率显著提升, 效率提升了大致300倍
Time forloop: 3.23 Time vector: 0.01
例2. u = Av, u,v均为向量, A为矩阵, 例A的维度为2*3, v为3*1, 结果u为2*1
import numpy as np
def vector():
A = np.array([[1,2,3],[4,5,6]])
v = np.array([[4],[5],[6]])
u = np.zeros((2,1))
u = np.dot(A,v)
print(u)
def forloop():
A = [
[1,2,3],
[4,5,6],
]
v = [
[4],
[5],
[6],
]
u = [
[0],
[0],
]
for i in range(len(A)):
for j in range(len(A[i])):
print(A[i][j])
print(v[j][0])
u[i][0] += A[i][j] * v[j][0]
print(u)例3. 有一个向量v, 想对v的每个元素做指数运算
u = np.exp(v)numpy库中还有很多向量函数np.log(), np.abs()......
Z = np.dot(w.T, X) + b
b是一个实数(1*1的矩阵), 但是当向量加上一个实数时, python会自动把这个实数扩展成一个1*m的行向量
dw = 1/m * X * dz.T
db = 1/m * np.sum(dZ)
循环方法
J,dw1,dw2,db = 0,0,0,0
for i in range(0,m):
z[i] = w*x[i] + b
a[i] = sigmoid(z[i])
J += -(y[i]*log(a[i]) + (1-y[i])*log(1-a[i]))
dz[i] = a[i] - y[i]
dw1 += x1[i] * dz[i]
dw2 += x2[i] * dz[i]
db += dz[i]
J /= m
dw1 /= m
dw2 /= m
db /=m
w -= alpha * dw
b -= alpha * db使用向量表示
# 对训练样本进行预测和求导
Z = np.dot(w.T, X) + b
A = 𝜎(Z)
dZ = A - Y
dw = 1/m * X * dz.T
db = 1/m * np.sum(dZ)
# 梯度下降更新参数
w -= alpha * dw
b -= alpha * db例. 计算不同食物中不同营养恒分中的卡了压力百分比
import numpy as np
A = np.array([[56.0, 0.0, 4.4, 68.0],
[1.2, 104.0, 52.0, 8.0],
[1.8, 135.0, 99.0, 0.9]])
cal = A.sum(axis = 0) # 0为按列计算, 1为按行计算
percentage = A / cal.reshape(1,4)
print(percentage)- 比如计算苹果中卡路里所占的百分比, 先计算56.0+1.2+1.8 = 59; 56/59 = 0.949
- 计算百分比时: 将3*4的矩阵A初一一个1*4的矩阵, 得到了一个3*4的结果矩阵, 即为所求
- 理论上
cal本身是一个1*4的向量, 不需要再进行reshape, 但是当我们写代码不确定矩阵维度的时候, 可以对矩阵进行重塑来确保得到我们想要的矩阵, 而reshape的时间复杂度是O(1), 调用代价极低
广播机制
-
一个4*1的列向量与一个常数做加法时, 会将常数扩展为一个4*1的列向量, 然后再按照矩阵的加法进行
-
广播机制对与列向量和行向量均可以使用
-
后缘维度的轴长度:
A.shape[-1], 即列数;如果两个数组的后院维度的轴长度相符或其中一方的轴长度为1, 则认为他们是广播兼容的, 广播会在缺失维度和轴长度为1的维度上进行*
卡路里的例子中A34的后缘维度的轴长度等于4; 而cal14的后缘维度也是4, 二者的后缘维度轴长度相符, 因此可以进行广播
广播会在轴长度为1的维度对应
axis=0即垂直方向, 复制成cal_temp3*4, 之后二者再进行运算
-
巨大的灵活性
-
不熟悉的话可能有奇怪的bug
比如一个n维列向量加上一个n维行向量, 不会报维度不匹配或类型错误之类的错误, 而是得到了广播后的结果
import numpy as np
A = np.array([1,2,3])
B = np.array([[1],[2],[3]])
result = A + B
print(result)
'''
Output:
[[2 3 4]
[3 4 5]
[4 5 6]]
'''一维数组 ❗❗❗**(在神经网络中不要使用)**
- 它不是行向量也不是列向量
- 转置后跟它本身看起来一样
- a乘以a的转置返回的是内积 --> 一个数
import numpy as np
a = np.random.randn(5)
print(a) # [-1.225 0.282 -0.958 1.176 -0.707]
print(a.shape) # (5,)
print(a.T) # [-1.225 0.282 -0.958 1.176 -0.707]
print(np.dot(a, a.T)) # 4.385列向量
import numpy as np
a = np.random.randn(5,1)
print(a) '''
[[ 0.03078465]
[ 0.52937981]
[-1.29145158]
[-0.3743261 ]
[ 0.46156606]]
'''
print(a.shape) # (5,1)
print(a.T) # [[ 0.03078465 0.52937981 -1.29145158 -0.3743261 0.46156606]]
print(np.dot(a, a.T)) '''
[[ 9.47694739e-04 1.62967726e-02 -3.97568863e-02 -1.15234983e-02 1.42091501e-02]
[ 1.62967726e-02 2.80242978e-01 -6.83668388e-01 -1.98160677e-01 2.44343752e-01]
[-3.97568863e-02 -6.83668388e-01 1.66784719e+00 4.83424032e-01 -5.96090221e-01]
[-1.15234983e-02 -1.98160677e-01 4.83424032e-01 1.40120028e-01 -1.72776223e-01]
[ 1.42091501e-02 2.44343752e-01 -5.96090221e-01 -1.72776223e-01 2.13043229e-01]]
'''如果不确定行/列向量是否shape有第二个维度(不是一维数组), 可以加入断言assert(a.shape == (5,1)), 或者reshape a = np.random.randn(5).reshape(5,1)
-
升级最新版pip
-
查看python版本
-
安装Jupyter
安装成功
-
运行Jutyper Notebook
-
查看python版本
-
安装Jupyter
安装成功
-
运行Jutyper Notebook
-
新建笔记本
-
Code --- 写代码
Markdown --- 写文本, 运行一段代码后添加结论, 添加注释等
Raw NBConvert --- 将笔记本转换成另一种格式(如HTML)的命令行工具
Heading --- 添加标题
-
查看预定义的功能
-
逐行方式, 所有给定的命令必须以%开头
逐单元方式, 所有的命令必须以%%开头
-
快捷键:
Esc 和 Enter: 切换键盘输入模式-
命令(蓝色边框)
-
A: 当前单元之前插入一个新单元 -
B: 当前单元之后插入一个新单元 -
DD: 删除当前单元 -
Z: 撤销被删除的单元 -
Y: 将当前活跃的单元变成一个代码单元 -
F: 查找和替换 -
Shift + ↑ / ↓: 选择多个单元Shift + M: 将多个单元合并 -
H: 查看快捷键
-
-
编辑(绿色边框)
-
Ctrl + Enter: 运行代码块 -
Alt + Enter: 运行单元, 并在下面添加一个新单元 -
Ctrl + Shift + F: 打开命令面板
-
-
始于Jupyter Notebooks:一份全面的初学者实用指南
-
输入层
-
隐藏层: 在训练集中不知道它们的准确值
-
输出层: 产生预测值
-
激活值:a[i]表示输入特征 (a是激活的意思,意味着网络中不同层的值回传递到后面的层中)
- 输入层的激活值为a[0]
- 隐藏层的第一个结点的激活值记为a1[0],所以a[1]是一个大小为4的列向量
- 输出层的激活值a[2]即为我们要的$\hat{y}$
-
x表示输入特征
-
a表示每个神经元的输出
-
W表示特征的权重;上标表示神经网络的层数,下表表示该层的第几个神经元
说明:
- 这是一个两层的神经网络(通常输入层不算入其中)
- 隐藏层和输出层是带有参数的
- 隐藏层有参数W[1]和b[1],W是一个4*3的矩阵,b是一个4*1的向量;4是隐藏层单元的结点数,3是因为有三个输入特征
- 输出层有与之关联的W[2]和b[2],大小分别为1*4和1*1;该层有1个结点,上一层有4个结点
- 按步骤计算出z
- 以sigmoid函数为激活函数计算z(得出a)
- 重复这个过程
两层的神经网络:
- 计算$z_{1}^{[1]}, z_{1}^{[1]}=w_{1}^{[1] T} x+b_{1}^{[1]}$
- 通过激活函数计算$a_{1}^{[1]}, a_{1}^{[1]}=\sigma\left(z_{1}^{[1]}\right)$
- 重复这个过程, 分别计算$a_{2}^{[1]}, a_{3}^{[1]}, a_{4}^{[1]}$
向量化计算:
将神经网络中的一层神经元参数纵向堆积起来
例如隐藏层中的w纵向堆积起来变成4*3的矩阵, 用W[1]表示
在这个两层的神经网络中, 输入x可以表示为$a^{[0]}$, 最终的输出为$\hat{y}=a^{[2]}$
最终的计算过程:
- 和“AI是新电力”相类似的说法是什么?
【 】AI为我们的家庭和办公室的个人设备供电,类似于电力。 【 】通过“智能电网”,AI提供新的电能。 【 】AI在计算机上运行,并由电力驱动,但是它正在让以前的计算机不能做的事情变为可能。 【 ✔ 】就像100年前产生电能一样,AI正在改变很多的行业。 请注意: 吴恩达在视频中表达了同样的观点。
- 哪些是深度学习快速发展的原因? (两个选项)
【✔ 】 现在我们有了更好更快的计算能力。 【 】神经网络是一个全新的领域。 【 ✔】 我们现在可以获得更多的数据。 【 】深度学习已经取得了重大的进展,比如在在线广告、语音识别和图像识别方面有了很多的应用。
- 回想一下关于不同的机器学习思想的迭代图。下面哪(个/些)陈述是正确的?
【 ✔】能够让深度学习工程师快速地实现自己的想法。 【 ✔】在更好更快的计算机上能够帮助一个团队减少迭代(训练)的时间。 【 】在数据量很多的数据集上训练上的时间要快于小数据集。 【 ✔】 使用更新的深度学习算法可以使我们能够更快地训练好模型(即使更换CPU / GPU硬件)。 请注意: 同一模型在较大的数据集上通常需要花费更多时间。
- 当一个经验丰富的深度学习工程师在处理一个新的问题的时候,他们通常可以利用先前的经验来在第一次尝试中训练一个表现很好的模型,而不需要通过不同的模型迭代多次从而选择一个较好的模型,这个说法是正确的吗?
【 】正确 【 ✔】 错误 请注意:也许之前的一些经验可能会有所帮助,但没有人总是可以找到最佳模型或超参数而无需迭代多次。
- 这些图中的哪一个表示ReLU激活功能?

所有负值都变为0, 而正值不变, 这个特性称为单侧抑制, 使得神经网络中的神经元也具有了稀疏激活性
通过ReLU实现稀疏后的模型能够更好地挖掘相关特征,拟合训练数据
相比于其它激活函数来说,ReLU有以下优势:
-
对于线性函数而言,ReLU的表达能力更强,尤其体现在深度网络中;
-
而对于非线性函数而言,ReLU由于非负区间的梯度为常数,因此不存在梯度消失问题,使得模型的收敛速度维持在一个稳定状态。
梯度消失问题:当梯度小于1时,预测值与真实值之间的误差每传播一层会衰减一次,如果在深层模型中使用sigmoid作为激活函数,这种现象尤为明显,将导致模型收敛停滞不前。
- 用于识别猫的图像是“结构化”数据的一个例子,因为它在计算机中被表示为结构化矩阵,是真的吗?
【 】正确 【 ✔】 错误 博主注:图片属于非结构化数据。
- 统计不同城市人口、人均GDP、经济增长的人口统计数据集是“非结构化”数据的一个例子,因为它包含来自不同来源的数据,是真的吗?
【 】正确 【 ✔】 错误 博主注:单纯的看以上数据的话就是非结构化数据,但是这些数据都被整合到了数据集里面,所以是结构化数据。
- 为什么在上RNN(循环神经网络)可以应用机器翻译将英语翻译成法语?
【❗ ✔】 因为它可以被用做监督学习。 【 】严格意义上它比卷积神经网络(CNN)效果更好。 【❗ ✔】 它比较适合用于当输入/输出是一个序列的时候(例如:一个单词序列) 【 ❌】RNNs代表递归过程:想法->编码->实验->想法->…
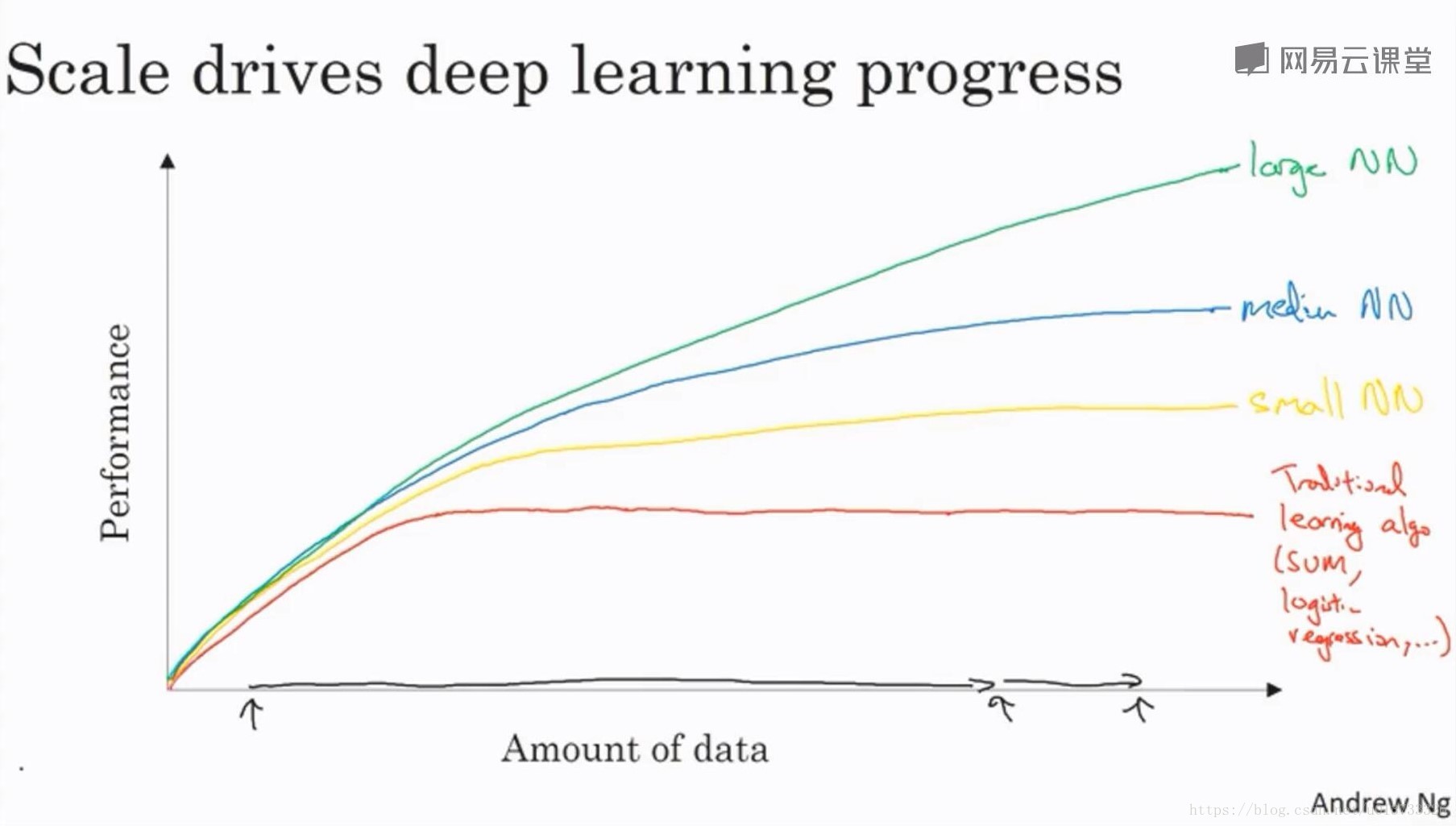
-
在我们手绘的这张图中,横轴(x轴)和纵轴(y轴)代表什么?
x轴是数据量 y轴是不同算法的表现能力
- 假设上一个问题图中描述的是准确的(并且希望您的轴标签正确),以下哪一项是正确的?
【 ✔】 增加训练集的大小通常不会影响算法的性能,这可能会有很大的帮助。 【 ✔】 增加神经网络的大小通常不会影响算法的性能,这可能会有很大的帮助。 【 】减小训练集的大小通常不会影响算法的性能,这可能会有很大的帮助。 【 】减小神经网络的大小通常不会影响算法的性能,这可能会有很大的帮助。
- 神经元节点计算什么?
【 】神经元节点先计算激活函数,再计算线性函数(z = Wx + b)
【 ✔】神经元节点先计算线性函数(z = Wx + b),再计算激活。
【 】神经元节点计算函数g,函数g计算(Wx + b)。
【 】在将输出应用于激活函数之前,神经元节点计算所有特征的平均值
请注意:神经元的输出是a = g(Wx + b),其中g是激活函数(sigmoid,tanh,ReLU,…)。
-
下面哪一个是Logistic损失?
略
-
假设img是一个(32,32,3)数组,具有3个颜色通道:红色、绿色和蓝色的32x32像素的图像。 如何将其重新转换为列向量?
x = img.reshape(32 * 32 * 3, 1)
# 或
x = img.reshape(-1, 1)Jupyter Notebook
import numpy as np
img = np.random.randint(0,100,(3,3,2))初始化img为(3,3,2)大小的三维向量
print(img)[[[ 4 87]
[92 5]
[83 53]]
[[72 31]
[72 47]
[21 84]]
[[53 27]
[32 96]
[39 33]]]
print(img.shape)(3, 3, 2)
shaped_img = img.reshape(3*3*2,1)将其转化为列向量
print('after shape: ')
print(shaped_img)after shape:
[[ 4]
[87]
[92]
[ 5]
[83]
[53]
[72]
[31]
[72]
[47]
[21]
[84]
[53]
[27]
[32]
[96]
[39]
[33]]
print(shaped_img.shape)(18, 1)
另一种转化为列向量的方式
shaped_img2 = img.reshape(-1,1)print('second shape:')
print(shaped_img2)
print(shaped_img2.shape)second shape:
[[ 4]
[87]
[92]
[ 5]
[83]
[53]
[72]
[31]
[72]
[47]
[21]
[84]
[53]
[27]
[32]
[96]
[39]
[33]]
(18, 1)
-
看一下下面的这两个随机数组“a”和“b”:
a = np.random.randn(2, 3) # a.shape = (2, 3) b = np.random.randn(2, 1) # b.shape = (2, 1) c = a + b
请问数组c的维度是多少?
答:b的后缘维度为1, 二者是广播兼容的, 广播在缺失维度上进行, 将b复制3次扩展为(2, 3)之后再与a做矩阵加法运算, 所以最终c的维度是(2,3) c.shape = (2,3)
-
看一下下面的这两个随机数组“a”和“b”:
a = np.random.randn(4, 3) # a.shape = (4, 3) b = np.random.randn(3, 2) # b.shape = (3, 2) c = a * b
请问数组“c”的维度是多少?
答:二者的后缘维度不相符且没有一方的轴长度为1, 因此二者不是广播兼容的, 因此运行会出错, 无法计算 ValueError: operands could not be broadcast together with shapes (4,3) (3,2)
定义了CNN的基本组件, 是CNN的鼻祖
卷积层、池化层、全连接层
- 输入的图像是28*28像素的图像, 用矩阵表示为[1, 28, 28]
- 第一个卷积层所用的卷积核为5 * 5, 滑动步长为1, 卷积核数目为20; 经过该层后图像尺寸变为(28-5+1=24), 输出矩阵为[20, 24, 24]
- 第一个池化层pool核尺寸为2*2, 步长为2, 池化操作后, 图像尺寸减半, 输出矩阵为[20, 12, 12]
- 第一个卷积层所用的卷积核为5 * 5, 滑动步长为1, 卷积核数目为50; 经过该层后图像尺寸变为(12-5+1=8), 输出矩阵为[50, 8, 8]
- 第二个池化层pool核尺寸为2*2, 步长为2, 池化操作后, 图像尺寸减半, 输出矩阵为[50, 4, 4]
- 第一个全连接层, 神经元数目为500, 再接
relu激活函数 - 第二个全连接层, 神经元个数为10, 用于10个数字的训练, 再接
softmax函数, 最终得到分类的概率
def LeNet():
model = Sequential()
model.add(Conv2D(32,(5,5),strides=(1,1),input_shape=(28,28,1),padding='valid',activation='relu',kernel_initializer='uniform'))
model.add(MaxPooling2D(pool_size=(2,2)))
model.add(Conv2D(64,(5,5),strides=(1,1),padding='valid',activation='relu',kernel_initializer='uniform'))
model.add(MaxPooling2D(pool_size=(2,2)))
model.add(Flatten())
model.add(Dense(100,activation='relu'))
model.add(Dense(10,activation='softmax'))
return model- 更深的网络
- 数据增广来增加模型的泛化能力
- 用ReLU代替Sigmoid来加快SGD的收敛速度
- Dropout防止模型过拟合
- LRN
<a name="AlexNet模型>
-
前面5层是卷积层, 后面三层是全连接层, 最终
softmax输出是1000类 -
输入图片为256*256的三通道彩色照片, 为了增强模型的泛化能力, 避免过拟合, 使用随机裁剪得到3*224*224的图像, 作为网络的输入
-
使用GPU再第一层卷积层后有两个完全一样的分支加速训练
def AlexNet():
model = Sequential()
model.add(Conv2D(96,(11,11),strides=(4,4),input_shape=(227,227,3),padding='valid',activation='relu',kernel_initializer='uniform'))
model.add(MaxPooling2D(pool_size=(3,3),strides=(2,2)))
model.add(Conv2D(256,(5,5),strides=(1,1),padding='same',activation='relu',kernel_initializer='uniform'))
model.add(MaxPooling2D(pool_size=(3,3),strides=(2,2)))
model.add(Conv2D(384,(3,3),strides=(1,1),padding='same',activation='relu',kernel_initializer='uniform'))
model.add(Conv2D(384,(3,3),strides=(1,1),padding='same',activation='relu',kernel_initializer='uniform'))
model.add(Conv2D(256,(3,3),strides=(1,1),padding='same',activation='relu',kernel_initializer='uniform'))
model.add(MaxPooling2D(pool_size=(3,3),strides=(2,2)))
model.add(Flatten())
model.add(Dense(4096,activation='relu'))
model.add(Dropout(0.5))
model.add(Dense(4096,activation='relu'))
model.add(Dropout(0.5))
model.add(Dense(1000,activation='softmax'))
return model在加深网络的同时, 引入Inception结构代替了单纯的卷积激活的传统操作
- 引入Inception结构
- 中间层的辅助LOSS单元
- 后面的全连接层全部替换为简单的全局平均pooling
- 卷积stride都是1
- 为了保持特征相应图大小一致, 都用0填充
- 每个卷积层后面都立即接一个
relu函数, 并把4组不同类型但大小相同的特征相应图一张张并排叠起来, 形成新的特征相应图 -
主要功能:
- 通过3*3的池化, 以及1*1、3*3、5*5三种不同尺度的卷积核, 一共4中方式对输入的特征相应图做了特征提取
- 采用1*1卷积核实现降维, 同时让信息通过更少的连接传递以达到更加稀疏的特性
- 网络结构中有3个LOSS单元, 这样做是为了帮助网络的收敛: 在中间层加入腐竹计算的LOSS单元, 使得计算损失时让低层的特征有很好的区分能力, 从而让网络更好的被训练
- 后面的全连接层全部替换为简单的全局平均pooling
def Conv2d_BN(x, nb_filter,kernel_size, padding='same',strides=(1,1),name=None):
if name is not None:
bn_name = name + '_bn'
conv_name = name + '_conv'
else:
bn_name = None
conv_name = None
x = Conv2D(nb_filter,kernel_size,padding=padding,strides=strides,activation='relu',name=conv_name)(x)
x = BatchNormalization(axis=3,name=bn_name)(x)
return x
def Inception(x,nb_filter):
branch1x1 = Conv2d_BN(x,nb_filter,(1,1), padding='same',strides=(1,1),name=None)
branch3x3 = Conv2d_BN(x,nb_filter,(1,1), padding='same',strides=(1,1),name=None)
branch3x3 = Conv2d_BN(branch3x3,nb_filter,(3,3), padding='same',strides=(1,1),name=None)
branch5x5 = Conv2d_BN(x,nb_filter,(1,1), padding='same',strides=(1,1),name=None)
branch5x5 = Conv2d_BN(branch5x5,nb_filter,(1,1), padding='same',strides=(1,1),name=None)
branchpool = MaxPooling2D(pool_size=(3,3),strides=(1,1),padding='same')(x)
branchpool = Conv2d_BN(branchpool,nb_filter,(1,1),padding='same',strides=(1,1),name=None)
x = concatenate([branch1x1,branch3x3,branch5x5,branchpool],axis=3)
return x
def GoogLeNet():
inpt = Input(shape=(224,224,3))
#padding = 'same',填充为(步长-1)/2,还可以用ZeroPadding2D((3,3))
x = Conv2d_BN(inpt,64,(7,7),strides=(2,2),padding='same')
x = MaxPooling2D(pool_size=(3,3),strides=(2,2),padding='same')(x)
x = Conv2d_BN(x,192,(3,3),strides=(1,1),padding='same')
x = MaxPooling2D(pool_size=(3,3),strides=(2,2),padding='same')(x)
x = Inception(x,64)#256
x = Inception(x,120)#480
x = MaxPooling2D(pool_size=(3,3),strides=(2,2),padding='same')(x)
x = Inception(x,128)#512
x = Inception(x,128)
x = Inception(x,128)
x = Inception(x,132)#528
x = Inception(x,208)#832
x = MaxPooling2D(pool_size=(3,3),strides=(2,2),padding='same')(x)
x = Inception(x,208)
x = Inception(x,256)#1024
x = AveragePooling2D(pool_size=(7,7),strides=(7,7),padding='same')(x)
x = Dropout(0.4)(x)
x = Dense(1000,activation='relu')(x)
x = Dense(1000,activation='softmax')(x)
model = Model(inpt,x,name='inception')
return model为了解决初始化等问题, VGG采用pre-training的方式: 先训练一部分小网络, 在确保这部分网络稳定之后, 再在此基础上逐渐加深
- 卷积层都是相同的卷积, 因此卷积过后输出图像的尺寸与输入是一只的
- 下采样完全是有max pooling实现的
- VGG网络后接三个全连接层, filter(卷积后的输出通道数)个数从64开始, 每接一个pooling后成倍增加
- 卷积层使用更小的filter尺寸和间隔
- 多个3*3的卷积层比一个大尺寸filter卷积层有更多的非线性, 是的判决函数更加具有判决行
- 多个3*3的卷积层比一个大尺寸filter卷积层油更少的参数
- 1*1卷积核课在不影响输入输出维数的情况下, 对输入进行线性形变, 然后通过
relu进行非线性处理, 增加网络的非线性表达能力
def VGG_16():
model = Sequential()
model.add(Conv2D(64,(3,3),strides=(1,1),input_shape=(224,224,3),padding='same',activation='relu',kernel_initializer='uniform'))
model.add(Conv2D(64,(3,3),strides=(1,1),padding='same',activation='relu',kernel_initializer='uniform'))
model.add(MaxPooling2D(pool_size=(2,2)))
model.add(Conv2D(128,(3,2),strides=(1,1),padding='same',activation='relu',kernel_initializer='uniform'))
model.add(Conv2D(128,(3,3),strides=(1,1),padding='same',activation='relu',kernel_initializer='uniform'))
model.add(MaxPooling2D(pool_size=(2,2)))
model.add(Conv2D(256,(3,3),strides=(1,1),padding='same',activation='relu',kernel_initializer='uniform'))
model.add(Conv2D(256,(3,3),strides=(1,1),padding='same',activation='relu',kernel_initializer='uniform'))
model.add(Conv2D(256,(3,3),strides=(1,1),padding='same',activation='relu',kernel_initializer='uniform'))
model.add(MaxPooling2D(pool_size=(2,2)))
model.add(Conv2D(512,(3,3),strides=(1,1),padding='same',activation='relu',kernel_initializer='uniform'))
model.add(Conv2D(512,(3,3),strides=(1,1),padding='same',activation='relu',kernel_initializer='uniform'))
model.add(Conv2D(512,(3,3),strides=(1,1),padding='same',activation='relu',kernel_initializer='uniform'))
model.add(MaxPooling2D(pool_size=(2,2)))
model.add(Conv2D(512,(3,3),strides=(1,1),padding='same',activation='relu',kernel_initializer='uniform'))
model.add(Conv2D(512,(3,3),strides=(1,1),padding='same',activation='relu',kernel_initializer='uniform'))
model.add(Conv2D(512,(3,3),strides=(1,1),padding='same',activation='relu',kernel_initializer='uniform'))
model.add(MaxPooling2D(pool_size=(2,2)))
model.add(Flatten())
model.add(Dense(4096,activation='relu'))
model.add(Dropout(0.5))
model.add(Dense(4096,activation='relu'))
model.add(Dropout(0.5))
model.add(Dense(1000,activation='softmax'))
return model- 层数非常深, 已经超过百层
- 引入残差单元来解决退化问题
-
数据经过了两条路线,一条是常规路线,另一条则是捷径(shortcut),直接实现单位映射的直接连接的路线,类似与电路中的“短路”
-
把网络中的一个模块的输入和输出关系看作是y=H(x),那么直接通过梯度方法求H(x)就会遇到退化问题,如果使用带shortcut的结构,那么可变参数部分的优化目标就不再是H(x), 若用F(x)来代表需要优化的部分的话,则
H(x)=F(x)+x,也就是F(x)=H(x)-x -
在单位映射的假设中
y=x就相当于观测值,所以F(x)就对应着残差,因而叫残差网络 -
考虑到x的维度与F(X)维度可能不匹配情况,需进行维度匹配
- zero_padding:对恒等层进行0填充的方式将维度补充完整, 不会增加额外的参数
- projection:在恒等层采用1x1的卷积核来增加维度, 会增加额外的参数
-
残差模块:
- 常规残差模块,有两个3×3卷积核卷积核组成,但是随着网络进一步加深,这种残差结构在实践中并不是十分有效
- “瓶颈残差模块”可以有更好的效果,它依次由1×1、3×3、1×1这三个卷积层堆积而成,这里的1×1的卷积能够起降维或升维的作用,从而令3×3的卷积可以在相对较低维度的输入上进行,以达到提高计算效率的目的。
def Conv2d_BN(x, nb_filter,kernel_size, strides=(1,1), padding='same',name=None):
if name is not None:
bn_name = name + '_bn'
conv_name = name + '_conv'
else:
bn_name = None
conv_name = None
x = Conv2D(nb_filter,kernel_size,padding=padding,strides=strides,activation='relu',name=conv_name)(x)
x = BatchNormalization(axis=3,name=bn_name)(x)
return x
def Conv_Block(inpt,nb_filter,kernel_size,strides=(1,1), with_conv_shortcut=False):
x = Conv2d_BN(inpt,nb_filter=nb_filter[0],kernel_size=(1,1),strides=strides,padding='same')
x = Conv2d_BN(x, nb_filter=nb_filter[1], kernel_size=(3,3), padding='same')
x = Conv2d_BN(x, nb_filter=nb_filter[2], kernel_size=(1,1), padding='same')
if with_conv_shortcut:
shortcut = Conv2d_BN(inpt,nb_filter=nb_filter[2],strides=strides,kernel_size=kernel_size)
x = add([x,shortcut])
return x
else:
x = add([x,inpt])
return x
def ResNet50():
inpt = Input(shape=(224,224,3))
x = ZeroPadding2D((3,3))(inpt)
x = Conv2d_BN(x,nb_filter=64,kernel_size=(7,7),strides=(2,2),padding='valid')
x = MaxPooling2D(pool_size=(3,3),strides=(2,2),padding='same')(x)
x = Conv_Block(x,nb_filter=[64,64,256],kernel_size=(3,3),strides=(1,1),with_conv_shortcut=True)
x = Conv_Block(x,nb_filter=[64,64,256],kernel_size=(3,3))
x = Conv_Block(x,nb_filter=[64,64,256],kernel_size=(3,3))
x = Conv_Block(x,nb_filter=[128,128,512],kernel_size=(3,3),strides=(2,2),with_conv_shortcut=True)
x = Conv_Block(x,nb_filter=[128,128,512],kernel_size=(3,3))
x = Conv_Block(x,nb_filter=[128,128,512],kernel_size=(3,3))
x = Conv_Block(x,nb_filter=[128,128,512],kernel_size=(3,3))
x = Conv_Block(x,nb_filter=[256,256,1024],kernel_size=(3,3),strides=(2,2),with_conv_shortcut=True)
x = Conv_Block(x,nb_filter=[256,256,1024],kernel_size=(3,3))
x = Conv_Block(x,nb_filter=[256,256,1024],kernel_size=(3,3))
x = Conv_Block(x,nb_filter=[256,256,1024],kernel_size=(3,3))
x = Conv_Block(x,nb_filter=[256,256,1024],kernel_size=(3,3))
x = Conv_Block(x,nb_filter=[256,256,1024],kernel_size=(3,3))
x = Conv_Block(x,nb_filter=[512,512,2048],kernel_size=(3,3),strides=(2,2),with_conv_shortcut=True)
x = Conv_Block(x,nb_filter=[512,512,2048],kernel_size=(3,3))
x = Conv_Block(x,nb_filter=[512,512,2048],kernel_size=(3,3))
x = AveragePooling2D(pool_size=(7,7))(x)
x = Flatten()(x)
x = Dense(1000,activation='softmax')(x)
model = Model(inputs=inpt,outputs=x)
return model该数据集包含以下四个部分
- train-images-idx3-ubyte.gz: 训练集-图片,6w
- train-labels-idx1-ubyte.gz: 训练集-标签,6w
- t10k-images-idx3-ubyte.gz: 测试集-图片,1w
- t10k-labels-idx1-ubyte.gz: 测试集-标签,1w
每张图片大小为28*28像素, 可以用28*28大小的数组来表示一张图片
用大小为10的数组来表示
使用N位表示N种状态, 任何时候只有其中的一位有效
例如
性别:
[0, 1]代表女,[1, 0]代表男数字0-9: [0,0,0,0,0,0,0,0,0,1]代表9,[0,1,0,0,0,0,0,0,0,0]代表1
优点:
- 能够处理非连续性数值特征
- 一定程度上扩充了特征(性别本身是一个特征, 经过编码以后, 就变成了男或女两个特征)
- 容错性: 比如神经网络的输出结果是 [0,0.1,0.2,0.7,0,0,0,0,0, 0]转成独热编码后,表示数字3。即值最大的地方变为1,其余均为0。[0,0.1,0.4,0.5,0,0,0,0,0, 0]也能表示数字3。
- 在官网上下载
mnist.npz数据集 - 将其放于
~/.keras/datasets/mnist.npz中
- 输入: 传入给网络处理的向量, 784(2828)的向量*
- 输出: 网络处理后返回的结果: 大小为10的概率向量
- 标签: 期望网络返回的结果
作用: 评估网络模型的好坏
目标: 传入大量的训练集训练目标, 将损失函数的值降到最小
函数形式: -sum(label * log(y))
优点: 只关注独热编码中有效位的损失, 屏蔽了无效位的变化(不会影响最终的结果), 并且通过取对数放大了有效位的损失
例: [0, 0, 1] 与 [0.1, 0.3, 0.6]的交叉熵为 -log(0.6) = 0.51[0, 0, 1] 与 [0.2, 0.2, 0.6]的交叉熵为 -log(0.6) = 0.51[0, 0, 1] 与 [0.1, 0, 0.9]的交叉熵为 -log(0.9) = 0.10
作用: 如果把网络理解为一个函数, 回归模型是希望对这个函数进行拟合
方法: 不断地传入X和label的值, 来修正w和b, 使得最终得到的Y和label的loss最小
可以采用梯度下降法, 找到最快的方向, 调整w和b的值, 使得w*X + b的值越来越接近label
再计算交叉熵前的Y值是经过softmax后的,经过softmax后的Y,并不影响Y向量的每个位置的值之间的大小关系。但是有如下2个作用:
- 一是放大效果
- 二是梯度下降时需要一个可导的函数。
softmax函数将任意n维的实值向量转换为取值范围在(0,1)之间的n维实值向量,并且总和为1。
例如:向量softmax([1.0, 2.0, 3.0]) ------> [0.09003057, 0.24472847, 0.66524096]
性质:
- 因为softmax是单调递增函数,因此不改变原始数据的大小顺序。
- 将原始输入映射到(0,1)区间,并且总和为1,常用于表征概率。
- softmax(x) = softmax(x+c), 这个性质用于保证数值的稳定性。
import numpy as np
def softmax(x):
return np.exp(x) / np.sum(np.exp(x), axis=0)
softmax([4, 5, 10])
# [ 0.002, 0.007, 0.991]import numpy as np
import matplotlib.pyplot as plt
plt.rcParams['figure.figsize'] = (7,7) # Make the figures a bit bigger
from keras.datasets import mnist
from keras.models import Sequential
from keras.utils import np_utils # 使用one-hot 编码将输出标签的向量转化为布尔矩阵
from keras.layers.core import Dense, Dropout, Activation
'''
Dense: 全连接层
Dropout: 在训练过程中每次更新参数时按一定概率随机断开输入神经元, 防止过拟合
'''Using TensorFlow backend.
通过keras自带的数据集mnist导入数据, 对其进行归一化处理, 并将原而为数据变成一位数据, 作为网络的输入
nb_classes = 10
# the data, shuffled and split between tran and test sets
(X_train, y_train), (X_test, y_test) = mnist.load_data() # 加载数据
# 第一个tuple存储已经人工分类好的图片(每一个菇片都有自己对应的标签)
# 第二个tuple存储没分类的图片
print("X_train original shape", X_train.shape)
print("y_train original shape", y_train.shape)X_train original shape (60000, 28, 28)
y_train original shape (60000,)
X_train是list类型的对象, 存储的是28*28的图像像素
Y_train存储的是图像对应的标签(也就是该图片代表什么数字)
for i in range(9):
plt.subplot(3,3,i+1)
plt.imshow(X_train[i], cmap='gray', interpolation='none')
plt.title("Class {}".format(y_train[i]))对于每一个训练样本, 我们的神经网络的到单个的数组
- 先将28*28的图片变形成784长度的向量
X_train = X_train.reshape(60000, 784)
X_test = X_test.reshape(10000, 784)
X_train = X_train.astype('float32') # uint不能有负数, 要先转换为float类型
X_test = X_test.astype('float32')
# 给定的像素灰度是0~255, 为了使模型的巡训练效果更高, 通常将数值归一化映射到0-1
X_train /= 255
X_test /= 255
'''
可以以使用其他方法进行归一化
X_train = (X_train - 127) /127
X_test = (X_test - 127) / 127
'''
print("Training matrix shape", X_train.shape)
print("Testing matrix shape", X_test.shape)Training matrix shape (60000, 784)
Testing matrix shape (10000, 784)
- one-hot 编码: 再将输入从[0,255]压缩到[0,1]
0 -> [1,0,0,0,0,0,0,0,0]
1 -> [0,1,0,0,0,0,0,0,0]
2 -> [0,0,1,0,0,0,0,0,0]
etc.
Y_train = np_utils.to_categorical(y_train, nb_classes)
Y_test = np_utils.to_categorical(y_test, nb_classes)
# 建立一个Sequential模型, 然后一层层地加入神经元
model = Sequential()
'''
Dense层: 全连接层
所实现的运算是output = activation(dot(input, kernel)+bias)。其中activation是逐元素计算的激活函数,kernel是本层的权值矩阵,bias为偏置向量,只有当use_bias=True才会添加
units -> 512 代表该层的输出维度
'''
model.add(Dense(512, input_shape=(784,))) # 第一层要指定数据规模
'''
Activation层: 激活层
activation -> relu 将要使用的激活函数
'''
model.add(Activation('relu')) # An "activation" is just a non-linear function applied to the output
# of the layer above. Here, with a "rectified linear unit",
# we clamp all values below 0 to 0.
'''
Dropout层:
rate -> 0.2 在训练过程中每次更新参数时按此概率随机断开输入神经元, 防止过拟合
'''
model.add(Dropout(0.2)) # Dropout helps protect the model from memorizing or "overfitting" the training data
model.add(Dense(512))
model.add(Activation('relu'))
model.add(Dropout(0.2))
model.add(Dense(10))
model.add(Activation('softmax')) # This special "softmax" activation among other things,
# ensures the output is a valid probaility distribution, that is
# that its values are all non-negative and sum to 1.训练模型之前, 需要通过编译对学习过程进行配置
- 损失函数: 分类交叉熵(用于比较两个概率分布函数)
- 预测是个不同数字的概率分布, 目标是一个概率分布, 正确类别为100%, 其他所有类别为0
- 例如, 80%认为这个图片是3, 10%认为是2, 5%认为是1等
- 优化器: 帮助模型快速的学习, 同时防止“卡住”和“爆炸”情况
'''
损失函数loss: 模型试图最小化的目标函数设为categorical_crossentropy
优化器optimizer: 使用adam算法
指标列表metrics
'''
model.compile(loss='categorical_crossentropy', optimizer='adam', metrics=['accuracy'])'''
:param x: 如果模型只有一个输入, 那x应为numpy array, 如果模型有多个输入, 那x的类型应为list, list的元素是对应于各个输入的numpy array
:param y: 同x
:param batch_size: 指定进行梯度下降时每个batch包含的样本数; 训练时一个batch的样本会呗计算一次梯度下降, 使目标函数优化一步
:param epochs: 训练达到epoch值时停止
:param verbose: 日志显示(0=>不在标准输出流输出日志信息 1=>输出进度条记录 2=>每个epoch输出一行记录
:param validation_data: 验证集
'''
model.fit(X_train, Y_train,
batch_size=128, epochs=4,verbose=1,
validation_data=(X_test, Y_test))Train on 60000 samples, validate on 10000 samples
Epoch 1/4
60000/60000 [==============================] - 3s 45us/step - loss: 0.2525 - acc: 0.9235 - val_loss: 0.1099 - val_acc: 0.9657
Epoch 2/4
60000/60000 [==============================] - 2s 39us/step - loss: 0.1028 - acc: 0.9686 - val_loss: 0.0735 - val_acc: 0.9770
Epoch 3/4
60000/60000 [==============================] - 2s 41us/step - loss: 0.0704 - acc: 0.9782 - val_loss: 0.0666 - val_acc: 0.9786
Epoch 4/4
60000/60000 [==============================] - 3s 52us/step - loss: 0.0573 - acc: 0.9814 - val_loss: 0.0798 - val_acc: 0.9746
score = model.evaluate(X_test, Y_test, verbose=0)
print('Test score:', score[0])
print('Test accuracy:', score[1])Test score: 0.07981417043644469
Test accuracy: 0.9746
- 正确的例子
- 错误的例子
# The predict_classes function outputs the highest probability class
# according to the trained classifier for each input example.
predicted_classes = model.predict_classes(X_test)
# Check which items we got right / wrong
correct_indices = np.nonzero(predicted_classes == y_test)[0]
incorrect_indices = np.nonzero(predicted_classes != y_test)[0]plt.figure()
for i, correct in enumerate(correct_indices[:9]):
plt.subplot(3,3,i+1)
plt.imshow(X_test[correct].reshape(28,28), cmap='gray', interpolation='none')
plt.title("Predicted {}, Class {}".format(predicted_classes[correct], y_test[correct]))
plt.figure()
for i, incorrect in enumerate(incorrect_indices[:9]):
plt.subplot(3,3,i+1)
plt.imshow(X_test[incorrect].reshape(28,28), cmap='gray', interpolation='none')
plt.title("Predicted {}, Class {}".format(predicted_classes[incorrect], y_test[incorrect]))from __future__ import print_function
import keras
from keras.datasets import mnist
from keras.models import Sequential
from keras.layers import Dense, Dropout, Flatten
from keras.layers import Conv2D, MaxPooling2D
from keras import backend as K
batch_size = 128
num_classes = 10
epochs = 12
# input image dimensions
img_rows, img_cols = 28, 28Using TensorFlow backend.
# the data, split between train and test sets
(x_train, y_train), (x_test, y_test) = mnist.load_data()
if K.image_data_format() == 'channels_first':
x_train = x_train.reshape(x_train.shape[0], 1, img_rows, img_cols)
x_test = x_test.reshape(x_test.shape[0], 1, img_rows, img_cols)
input_shape = (1, img_rows, img_cols)
else:
x_train = x_train.reshape(x_train.shape[0], img_rows, img_cols, 1)
x_test = x_test.reshape(x_test.shape[0], img_rows, img_cols, 1)
input_shape = (img_rows, img_cols, 1)x_train = x_train.astype('float32')
x_test = x_test.astype('float32')
x_train /= 255
x_test /= 255
print('x_train shape:', x_train.shape)
print(x_train.shape[0], 'train samples')
print(x_test.shape[0], 'test samples')x_train shape: (60000, 28, 28, 1)
60000 train samples
10000 test samples
# convert class vectors to binary class matrices
y_train = keras.utils.to_categorical(y_train, num_classes)
y_test = keras.utils.to_categorical(y_test, num_classes)模型的定义主要适用的keras.layers提供的Conv2D(卷积) 与 MaxPooling2D(池化)函数
CNN的输入是维度为(image_height, image_width, color_channels)的张亮
对于mnist数据集, 输入的张亮维度就是(28, 28, 1), 通过参数input_shape传给网络的第一层
model = Sequential()
# 第一层: 卷积层, 有32个滤波器, 卷积核大小为3*3, 32个, 第一层要输入训练图片的规模
model.add(Conv2D(32, kernel_size=(3, 3),
activation='relu',
input_shape=input_shape))
# 第二层: 卷积层, 卷积核大小为3*3 64个
model.add(Conv2D(64, (3, 3), activation='relu'))
# 第三层: 池化层, 使用MaxPooling, 大小为2*2
model.add(MaxPooling2D(pool_size=(2, 2)))
# 第四层: Dropout层, 对参数进行正则化防止模型过拟合
model.add(Dropout(0.25))
# 第五层: 将三维张亮转换为一维向量, 展开前张亮的维度是(12,12,64), 转化为一维(9216)
model.add(Flatten())
# 使用Dense构建了2层全相连层, 逐步将一位向量的位数从9216变为128, 最终变为10
# 第六层: 全向量层, 有128个神经元, 激活函数采用‘relu’
model.add(Dense(128, activation='relu'))
# 第七层: 训练过程中每次更新参数时随机断开输入神经元
model.add(Dropout(0.5))
# 第八层: 激活函数为softmax, 10位恰好对应0~9十个数字
model.add(Dense(num_classes, activation='softmax'))
# 打印定义的模型结构
model.summary()_________________________________________________________________
Layer (type) Output Shape Param #
=================================================================
conv2d_1 (Conv2D) (None, 26, 26, 32) 320
_________________________________________________________________
conv2d_2 (Conv2D) (None, 24, 24, 64) 18496
_________________________________________________________________
max_pooling2d_1 (MaxPooling2 (None, 12, 12, 64) 0
_________________________________________________________________
dropout_1 (Dropout) (None, 12, 12, 64) 0
_________________________________________________________________
flatten_1 (Flatten) (None, 9216) 0
_________________________________________________________________
dense_1 (Dense) (None, 128) 1179776
_________________________________________________________________
dropout_2 (Dropout) (None, 128) 0
_________________________________________________________________
dense_2 (Dense) (None, 10) 1290
=================================================================
Total params: 1,199,882
Trainable params: 1,199,882
Non-trainable params: 0
_________________________________________________________________
model.compile(loss=keras.losses.categorical_crossentropy,
optimizer=keras.optimizers.Adadelta(),
metrics=['accuracy'])每经过一层epoch, 模型训练遍历所有样本1次 batch_size设置为128, 即每次模型训练使用的样本数量为100 每经过一次epoch, 模型遍历训练集的60000歌样本, 每次训练使用128个样本, 即模型训练469次, 即损失函数经过469此批量梯度下降
model.fit(x_train, y_train,
batch_size=batch_size,
epochs=epochs,
verbose=1,
validation_data=(x_test, y_test))Train on 60000 samples, validate on 10000 samples
Epoch 1/12
60000/60000 [==============================] - 49s 813us/step - loss: 0.2657 - acc: 0.9191 - val_loss: 0.0558 - val_acc: 0.9811
Epoch 2/12
60000/60000 [==============================] - 50s 830us/step - loss: 0.0863 - acc: 0.9751 - val_loss: 0.0402 - val_acc: 0.9869
Epoch 3/12
60000/60000 [==============================] - 53s 892us/step - loss: 0.0654 - acc: 0.9806 - val_loss: 0.0360 - val_acc: 0.9876
Epoch 4/12
60000/60000 [==============================] - 53s 890us/step - loss: 0.0547 - acc: 0.9833 - val_loss: 0.0306 - val_acc: 0.9888
Epoch 5/12
60000/60000 [==============================] - 52s 864us/step - loss: 0.0469 - acc: 0.9859 - val_loss: 0.0306 - val_acc: 0.9884
Epoch 6/12
60000/60000 [==============================] - 50s 834us/step - loss: 0.0425 - acc: 0.9872 - val_loss: 0.0289 - val_acc: 0.9900
Epoch 7/12
60000/60000 [==============================] - 51s 850us/step - loss: 0.0373 - acc: 0.9887 - val_loss: 0.0315 - val_acc: 0.9882
Epoch 8/12
60000/60000 [==============================] - 52s 861us/step - loss: 0.0346 - acc: 0.9894 - val_loss: 0.0322 - val_acc: 0.9892
Epoch 9/12
60000/60000 [==============================] - 52s 860us/step - loss: 0.0307 - acc: 0.9905 - val_loss: 0.0269 - val_acc: 0.9910
Epoch 10/12
60000/60000 [==============================] - 52s 872us/step - loss: 0.0293 - acc: 0.9907 - val_loss: 0.0291 - val_acc: 0.9898
Epoch 11/12
60000/60000 [==============================] - 53s 882us/step - loss: 0.0277 - acc: 0.9914 - val_loss: 0.0257 - val_acc: 0.9917
Epoch 12/12
60000/60000 [==============================] - 52s 872us/step - loss: 0.0266 - acc: 0.9920 - val_loss: 0.0262 - val_acc: 0.9919
<keras.callbacks.History at 0x10250cdd0>
score = model.evaluate(x_test, y_test, verbose=0)
print('Test loss:', score[0])
print('Test accuracy:', score[1])Test loss: 0.026224144125275232
Test accuracy: 0.9919
import math
import matplotlib.pyplot as plt
import numpy as np
import random
'''画出单个数字'''
def drawDigit3(position, image, title, isTrue):
plt.subplot(*position) # 指定子图位置
plt.imshow(image.reshape(-1, 28), cmap='gray_r') # 把数字矩阵绘制成图
plt.axis('off') # 不显示坐标轴
# 如果预测正确则标题为黑色, 否则为红色
if not isTrue:
plt.title(title, color='red')
else:
plt.title(title)
def batchDraw3(batch_size, test_X, test_y):
selected_index = random.sample(range(len(test_y)), k=batch_size)
images = test_X[selected_index]
labels = test_y[selected_index]
predict_labels = model.predict(images)
image_number = images.shape[0]
row_number = math.ceil(image_number ** 0.5)
column_number = row_number
plt.figure(figsize=(row_number+8, column_number+8))
for i in range(row_number):
for j in range(column_number):
index = i * column_number + j
if index < image_number:
position = (row_number, column_number, index+1)
image = images[index]
actual = np.argmax(labels[index])
predict = np.argmax(predict_labels[index])
isTrue = actual==predict
title = 'actual:%d\npredict:%d' %(actual,predict)
drawDigit3(position, image, title, isTrue)
batchDraw3(20, x_test, y_test)
plt.show() 7月9号,在罗烨老师的办公室听完iLab实验室的介绍和相关方向的介绍后,我就决心加入ilab的暑期科研学习。多个方向的选择,多种算法和技术的学习也让我有很大的选择空间,加入ilab医学影像暑期科研是这个假期做过最有意义的事情。
从进入微信群之后,研究生学长就开始认真负责的给我们讲述这个假期的学习内容,让我在总体上有了一个认识“我这个假期到底要做什么事情?”,之后马上布置了第一周的任务,并把需要学习的电子书发到了群里。
第一周的学习内容主要围绕深度学习的入门,800多页的电子书不可能一个假期全部看完,而且新内容也是从未接触过的全新的知识,所以在一开始我就决心要啃一块硬骨头。慢,是每一步都走的扎实,从入门部分的每一个案例,每一个图表,每一段内容所讲授的核心知识点,我都把他们认真的整理成笔记,整理成笔记是一个梳理自己思维的最好方式,而且以后还可以一遍遍的查看,把新东西加进去,把老东西一遍遍的温习;在5天的学习过后我基本明白了深度学习所处理的内容、构建神经网络的过程、神经网络的编程基础(包括二分类、逻辑回归、代价函数、梯度下降、导数、计算图、向量化、广播)、以及搭建了Jupyter Notebook的环境,为进行专业的深度神经网络学习打下了很好的铺垫。
第一周快结束的时候我认真的做了这门课配套的第一周测试和第二周测试,在测试中查漏补缺,把自己认为自己已经熟练掌握的内容和知识点重新复习,也是更深入的了解,这样才能把学到的一些基础内容彻底消化;在做测试的时候也遇到很多问题,这些问题是之前没曾考虑过的,也是没遇到的,所以正是有了这两个小测验,让我把深度神经网络理论知识得到了全方位的学习。
在第一周中除了深度神经网络基础知识的学习外,我还对常用的网络结构进行了学习和整理,虽然现在还不是很能明白每个不同网络结构的细节和代码实现等部分;但是对于一个网络结构的组成,大致的执行过程以及不同网络结构的优缺点都有了一个全方位的理解。学习的过程总要是从入门到精通,从对这个领域未知,到对领域有一个朦朦胧胧的认知,再不断学习,反复更新自己的知识库,才能算是进入一个领域的大门,之后只有在这个领域不断的探索,不断的刷新知识的上限,才能在这个领域有所建树,出类拔萃。
第二周研究生学长了解完我们所学一周知识后的情况,为我们选择了MNIST手写数字的数据集进行深度神经网络的训练,虽然是最为最基础的数据集以及训练内容,但是对于一个只掌握了理论知识,从来还没进行过编码实现的新手来说还是很具有挑战的。在正式做之前,首先我阅读了大量的文章,弄明白MNIST数据集中数据的样子,编码方式等基础信息,只有对所处理的内容有一个全方位的了解,才能更好的实现深度神经网络;之后主要从两个方面进行MNIST数据集的训练,分别使用MLP多层神经网络和CNN卷积神经网络来实现手写数字的辨识,在这两种不同的网络的搭建过程中,不仅锻炼了我的python代码能力,更是让我充分的使用了Jupyter Notebook,最重要的是让我自己独立的搭建了神经网络,知道整体的构建过程,为我以后搭建更加复杂的神经网络打下了一个很好的底子。虽然这个项目不算复杂,但是学到的知识是可以很多元的,不仅把之前一周的理论知识融入了进来,而且把代码实现加了进来,把所有琐碎的知识点混在一起就能冲撞出别样的火花。
最后想感谢罗烨老师和研究生学长的认真负责,正是因为你们给了我这么好的交流环境以及把每个阶段的任务告诉我,我才能有明确的目标去完成好这次的暑期实习,同时也能有所收获,真的谢谢老师和学长。
这个暑期虽然不是在校外,在各大企业实习,但是在校内实验室的暑期实习同样让我对这个行业有了很深刻的了解。在学校平时的课程上,我们学习的更多是专业基础知识,就好比建筑一栋大楼的砖块的原材料,只有我们把这些原材料学好,才能学会做砖块的方法,才能在日后投入到企业中学会做高楼大厦的能力。这个假期在ilab实验室的暑期实习让我看到了我们这个专业更多的侧面,原来我们现在讨论的如此之火的人工智能深度学习大数据已经在医疗领域有了如此多的涉足,原来我们的传统医疗行业已经融入了如此之多的科技元素。 门诊领路者——智能导诊机器人,只需一句问候,即可“唤醒”,为患者提供预检分诊、自助挂号等服务。智慧病区,人工智能的集大成者。智能床垫,实时关注患者的生命体征,配合输液监控、病区综合护理管理看板、智能呼叫、电子床头屏等设备,病区医疗护理管理工作在数字化、智能化的帮助下形成了整体闭环。 虽然这些高尖端的技术我们作为新生不可能接触到,但是这些都是我们学校正在为医疗行业贡献的同济智慧。我们这个假期做的基础神经网络的训练,以及神经算法的简略版和基础知识,都是为这些技术打铺垫的很重要的一部分。 学习是为社会发展做铺垫的,我们在书本上学习的理论知识也不是凭空出来的,都是巨大的社会需求驱动的,所以我们课上所学的一些看似短期没什么用的课程,都是为了将来的某一部分社会需求服务,所以学好每一部分的知识,掌握好每一部分的能力真的更重要。深度神经网络只是入门,却没有终点,可以应用的领域和使用的价值还非常丰富,我们要做的就是把每一部分内容真正消化,将来能为我们的学校甚至是我们的好国家贡献一份力量。 每一个行业和领域都是永无止境的,软件这个行业当然也不是例外,就拿人工智能在医学领域的应用这一个侧面来说,我们能做的还很多很多,我们的社会医疗还可以有很大的提升空间,而接下来的一切都是科技进步的推动,有怎样的科学技术就会有怎么样的生产力,才会有怎么样方便舒适的社会生活。假想日后人工智能在医疗上取得了巨大的突破,那我们人类的一些疑难杂症也许就会得到进一步的之间,一些病情也会被尽早发现,尽早处理,人类在这一个从古至今梦寐以求征服的领域也许又会这下浓墨重彩的一笔。
这个暑期在学校的ilab实验室实习工作可以说是正经的第一份实习工作,这个假期跟着罗老师和助教学到了很多东西,也渐入深度神经网络的大门,在这个假期收获颇丰,但是一个假期的实习下来仍是有些问题希望可以得到老师和助教的解答。
- 第一周在看书的过程中,由于是新接触这个领域,对很多东西都不是很熟悉,所以速度比较慢,也很难抓得住重点,所以希望能得到老师或者学长的指导,要在哪些知识点上花苦功夫去啃,哪些细微的内容可以先粗略的知道,日后如果需要学习使用的时候再学习。
- 再一周过后没办法对自己的学习情况有一个掌握,虽然课后有两小节的习题,但是个人感觉远远不够,不足以检测出这一个阶段所学的内容是不是达到了标准。
- 在实战阶段,MNIST数据集手写数字识别作为入门是一个极佳的选择,在这个项目中开始真正的接触到了深度神经网络,也知道了如何搭建自己的网络去训练自己的数据集;但是是不是可以再进一步深入,让我们去了解更多这方面的知识,或者再多找些规模较小的项目让我们“练练手”呢?
- 学长让我们了解常用的网络结构,但是了解过后同样的是没办法了解自己到底有没有吃透这一部分内容,还是没办法进行一个很好的巩固和提升。
以上,是我个人对本次实习的一些浅薄的看法,希望老师不要介意,如果有任何不妥之处,也希望老师指出学生的问题,学生改正之后才能更好的成长。
一个假期的成果离不开老师的辛勤指导,感谢老师和助教,你们辛苦了。