En otros apuntes, hemos visto algoritmos que son poderosos para predecir valores desconocidos. Sin embargo, son de difícil visualización. Una de las técnicas clásicas para atender este problema son los árboles de decisión, el cual es uno de los enfoques clásicos en Machine Learning.
En este apunte encontrarás la explicación teorica y matemática de los árboles de decisión. En los apuntes, pasamos al código para ilustrar los temas cubiertos acá. Para este propósito usamos el data set Fish Market.
A diferencia de tutoriales pasados, en los últimos dos apuntes comparamos a Bagging y Boosting. Como veremos, son algoritmos que nos ayudan a potenciar a los árboles de decisión y generar una solución más robusta.
Si tienes alguna pregunta, no dudes en contactarme en Twitter: @XaviGrowth
Nota 1: La notación para vectores es en negritas. Es decir, podrás identificar a los vectores cuando aparezcan de la siguiente manera: y.
En tutoriales pasados hemos visto diferentes formas en las que podemos predecir datos futuros que son desconocidos. Y aunque regresión lineal y clasificación lineal son poderosos para solucionar ciertos problemas, pueden tener problemas en situaciones muy específicas.
Supongamos que queremos categorizar frutas por su dulzura. Para efectos de simpleza, solo distinguiremos entre naranjas y manzanas. Podemos en principio asignar pesos a un marcador de dulzura y usar regresión lineal para nuestras predicciones o catalogar cada fruta dentro de un plano usando KNN. Sin embargo, estos métodos fallarían de entrada al categorizar naranjas y manzanas. Aunque esto parece una obviedad, otros modelos lineales no empiezan categorizando.
En este punto, hay distinciones importantes entre casos por lo que los árboles de regresión son bastante útiles. Los árboles funcionan recursivamente dividiendo los datos en muchas categorias y luego asignando valores a cada data point que cae en cierta area. Aunque no es necesairamente el método más preciso, son una buena alternativa cuando lidiamos con versatilidad e interpretabilidad.
Cuando decimos que los árboles son generados recursivamente, nos referimos a que se dividen continuamente en el espacio donde están nuestros datos.
El punto final de un árbol son las hojas. Cada data point localizado en una hoja tiene un valor, que es el promedio de las hojas conocidas. Por ejemplo:
Suponiendo que la dulzura se mide según el nivel de sucrosa en un rango de 0 a 1, el valor en cada hoja es el promedio de los valores conocidas en ella. Todo junto representa los datos de entrenamiento que utilizaremos para generar un árbol de decisiones.
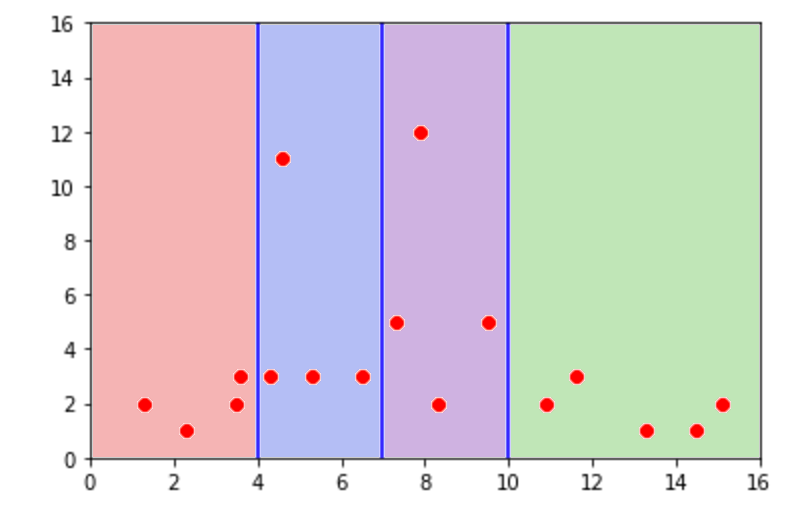
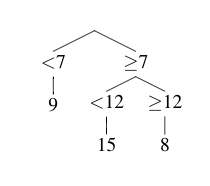
Esto también tiene repercusiones en el plano donde graficamos nuestros data points. Miremos el siguiente gráfico:
Si tuvieramos un valor x = 5 al que quisieramos ubicar, tendríamos solamente que seguir nuestro árbol. En este caso, x es mayor que 4 pero menor que y. Por tanto, sabemos que debe de caer en la zona azul. Para saber su valor en y, solo tenemos que sacar el promedio del resto de valores. Es decir:
y = 3 + 3 + 3 + 11 / 4 = 5
Para hacer el cálculo, tenemos que usar la fórmula de Suma de Errores Cuadrados (SEC) que vimos en regersión linear que se ve de la siguiente forma:
Aca la f (x) es la función representando nuestro árbol y cada punto está representado por variables predictoras xi y una variable resultante yi. En este sentido, para producir un buen árbol necesitamos un data set grande con valores resultantes conocidos que será nuestro set de entrenamiento.
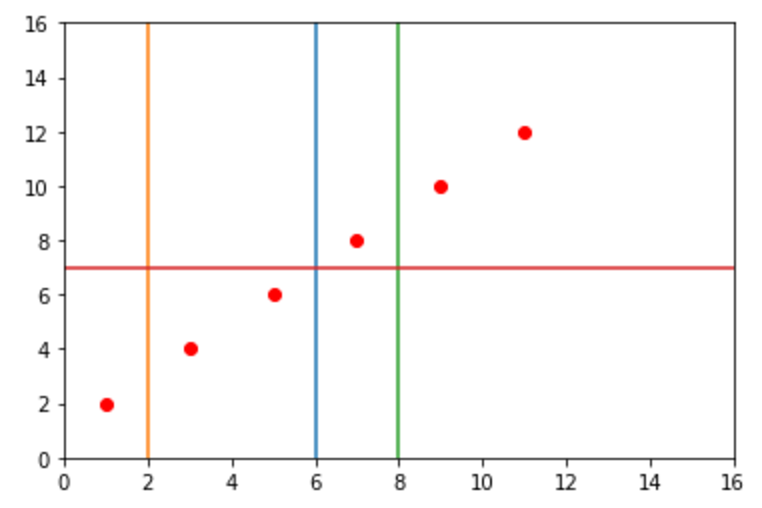
Para construir entonces un árbol tenemos que asumir que la mejor división es aquella que más minimiza la SEC. Usemos el siguiente gráfico:
En este caso sabemos que la línea azul hace el mejor trabajo reduciendo la SEC por las siguientes razones:
-
La línea roja puede ser descartada porque trata de dividir a través de variables resultantes, usando información para tratar de hacer estimaciones. Lo que lo hace una opción imposible.
-
Tenemos que generar una tabla que tenga promedios a la derecha e izquierda de cada línea en su eje y. Por ejemplo para la línea verde:
Valores a la izquierda en y: 8 + 6 + 4 + 2 / 4 = 5 Valores a la derecha en y: 10 + 22 / 2 = 11
Al completar la tabla tenemos los siguientes promedios, sus SEC y la SEC total.
| Valor Divisor | Promedio Izquierda | Promedio Derecha | SEC Izquierda | SEC Derecha | Total |
|---|---|---|---|---|---|
| 2 | 2 | 8 | 0 | 40 | 40 |
| 6 | 4 | 10 | 8 | 8 | 16 |
| 8 | 5 | 11 | 20 | 2 | 22 |
De esta manera, vemos que la línea divisora en x = 6 es la mejor ya que tiene la menor SEC.
Normalmente, dividir el plano nos ayuda a decrecer la SEC. En el ejemplo anterior podríamos tener hasta cinco divisiones, dado que el máximo de data points son seis. Es decir, siempre el máximo de secciones es la cantidad de datapoints en el eje x - 1. Sin embargo, hay que estar conscientes que este enfoque nos puede llevar a overfitting. Si añadimos suficientes hojas a nuestro árbol, podemos reducir el SEC hasta 0. Esta acción tiene efectos detrimentales:
- Se genera un sobreajuste y especialización en los datos de entrenamiento.
- Los errores en los datos que usamos para generar el árbol darán mucho peso a sus predicciones, dado que no hay valores con los cuales promediar.
- El desempeño con datos nuevos será malo.
La solución clásica a este problema es hacer crecer un árbol extensamente y luego cortar secciones hasta que se ajuste a nuestros deseos. Esto se hace con una función de costo que castiga la inexactitud y la complejidad. Si tomamos yi de cada data point y xi como la variable predictora, tenemos una f (x) en un subarbol que predice por yi y dentro del cual contiene un divisor T que se formularía asi:
Aquí, α es un parámetro de tunneo que controla que tanto castigamos la complejidad. Si α fuese al infinito, el número de hojas cortadas serían solo una ya que el costo de divisón se vuelve infinito. Dado que la SEC siempre será finita, el número de divisiones se acercará a 0 y el número de hojas se acercará a 1.
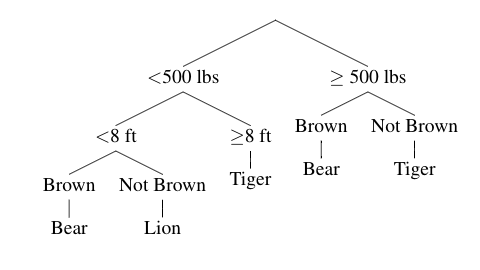
Uno de los usos más comúnes de los árboles de decisión es la clasificación. Esto es algo común, por ejemplo, en las clases de biología donde tenemos la manera en que se clasifican los seres vivos dependiendo del reino al que pertenecen. Estas son simples clasificaciones en donde las ramas se dispersan dependiendo de los observaciones. Por ejemplo:
Así como en los árboles de regresión, los árboles de clasificación están construidos con un conjunto de datos. Se usa para decidir que divisiones usar y como clasificar datos en las hojas al terminar el árbol. A cada hoja se le asigna cada punto que termina en cada clase, concentrándose en la clase más común.
Veamos la siguiente clasificación:
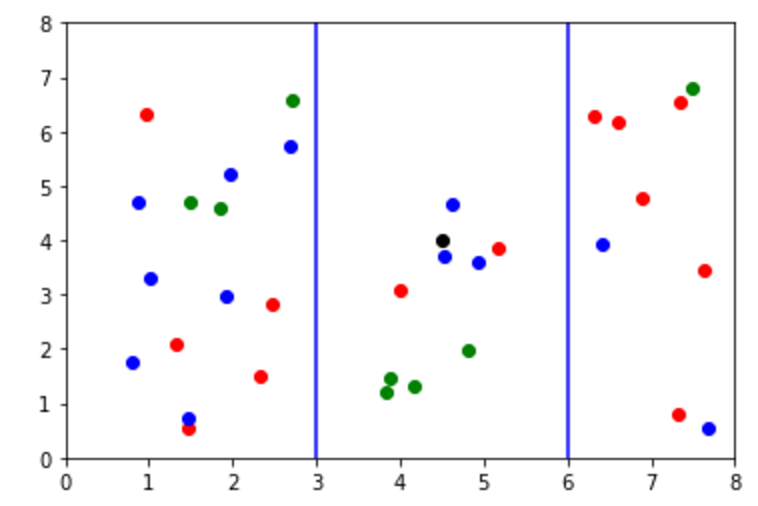
En este caso, tenemos tres categorías: azul, rojo y verde. El punto negro es un data point de clase desconocida. Si tuvieramos que clasificarlo, lo pondríamos dentro de la clase verde porque la mayoría de puntos en esta sección son verdes.
El proceso para crear árboles de clasificación es también recursivo. Empezamos definiendo una métrica que represente la calidad de la hoja en el árbol y seleccionamos repetidamente la división que mejor se ajusta a esta métrica. En este caso, empero, no podemos medir la SEC porque estamos tratando con datos cualitativos. Pero tenemos la alternativa de usar clases k a los que se les definen funciones de error m. Las funciones m más conocidas son:
- Tasa de Error Clasificatorio: la fracción de puntos mal representados.
- Índice Gini: que varía según el nivel de predicción de cada hoja.
- Entropia Cruzada: similar al Índice Gini, sin embargo se enfoca a medir el "ruido" en cada una de las hojas.
Cada una de estas utiliza Pmk como la proporción de puntos de clase k en una hoja m.
Si utilizacemos la Tasa de Error, podriamos formular una ecuación en donde N1 y N2 representan las hojas finales, mientras que E1 y E2 representan los errores al clasificar:
(N1 ⋅ E1) + (N2 ⋅ E2) / N1 + N2
Con esto tendríamos el promedio del peso de errores en contraposición al número de puntos. Sin embargo, el Índice Gini y la Entropia Cruzada son más usados para construir ábroles de decisión. Aunque suena contraintuitivo, la tasa de error solo se enfoca en reducir el error en los árboles de decisión. Tenemos que recordar que los árboles de decisión no toman en cuenta lo que sucede más adelante. En cambio, solo buscan solucionar un problema que sucede en el presente. Por ello, al usar el Índice Gini o la Entropía Cruzada aumentamos las posibilidades de crear divisiones que funcionen bien en el futuro.
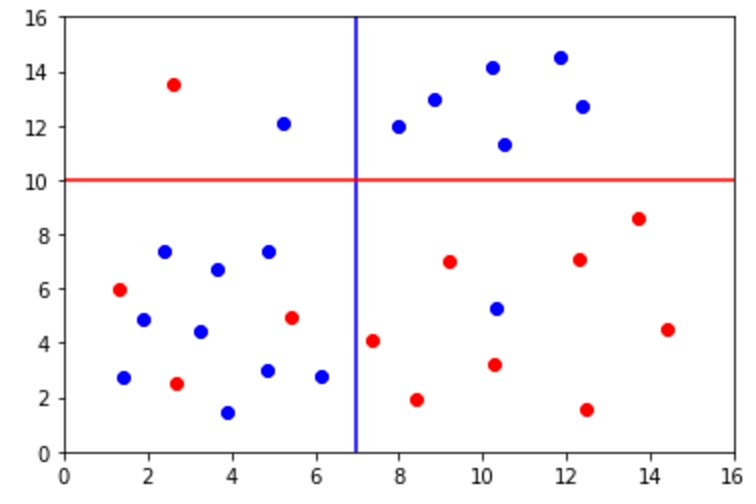
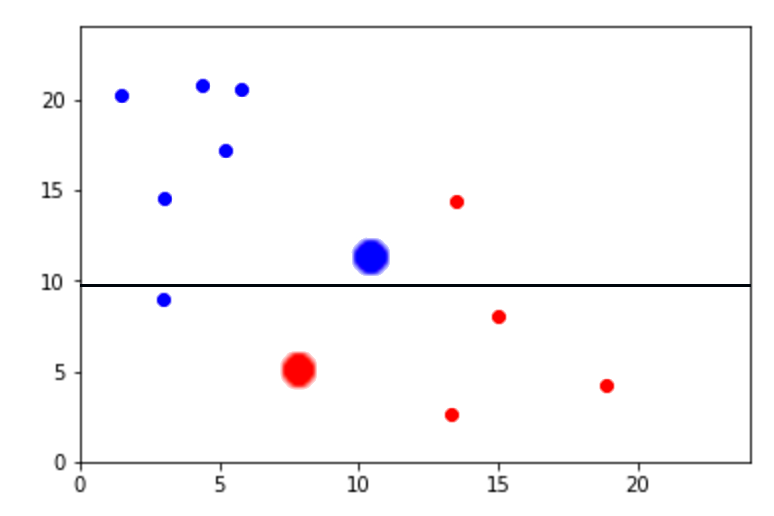
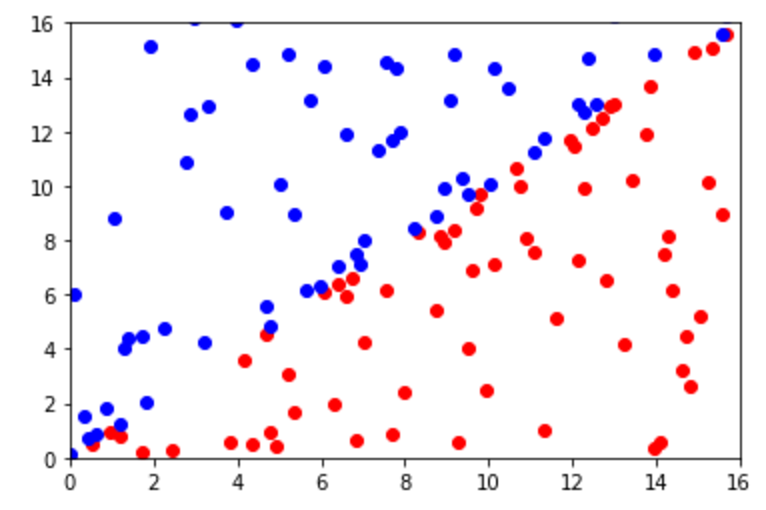
Una forma de visualizar como el Índice Gini elimina el ruido es con la siguiente gráfica:
Sin necesidad de usar fórmulas podemos ver que la línea azul en el eje x fue creada a partir de una tasa de error porque se enfocó en buscar un punto en donde se encontraban la mayoría de puntos rojos y azules. Sin embargo, podemos saber que la línea roja en el eje y fue creada con un Índice Gini y redujo el ruido de todos los puntos azules arriba de y = 10.
Al igual que sus pares en regresión, los árboles de clasificación caen fácilmente en overfitting. En esta sección del tuturoial hemos tratado al error de nuestros árboles como la proporción de puntos del data set de entrenamiendo que clasificó mal. Podemos recortar el árbol de varias maneras basado en esta función de error. Algunas soluciones pueden ser 1) añadir el total del número de hojas a la función de error e intentar minimizar la cantidad resultante o 2) cortar individualmente las hojas cuando sea necesario.
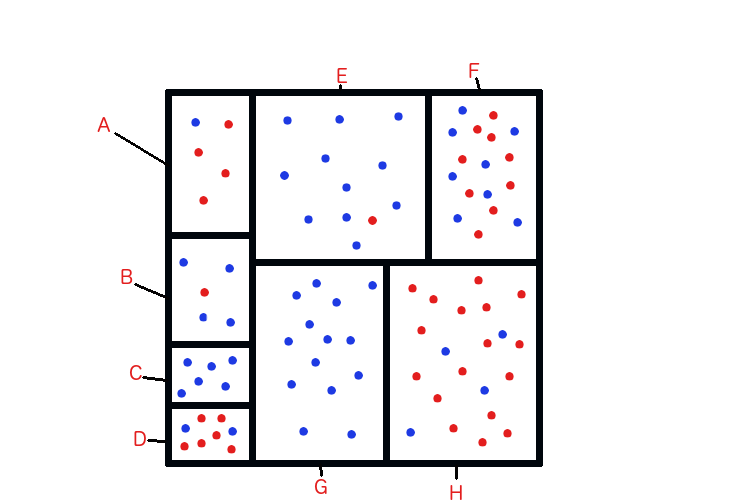
Tomemos el siguiente escenario:
Si quisieramos mezclar algunas de las secciones para evitar overfitting, deberíamos hacerlo con E y F. La razón es que dado que F tiene solo un punto azúl más y al combinarlo con E (que tiene mayormente puntos azules) solo causiaríamos una mala clasificación. La clave es contar la cantidad de puntos azules y rojos que habrían en otras combinaciones.
Pero ¿que sucedería si ignoraramos los datos de entrenamiento y crearamos un árbol arbitrariamente? ¿la tasa de error incrementaría con los datos de entrenamiento?
Hay que notar que la hoja original solo podrá dar puntos dentro de una clasificación, por lo que los puntos en la mayoría de una clase serán clasificados correctamente. Si tenemos una clase azul (mayoritaria) y otra roja (minoritaria), cada punto crearía dos clases nuevas. Si la hoja tiene más puntos azules que rojos, entonces nada cambia. Cada punto será clasificado correctamente solo si fue clasificado antes correctamente. Sin embargo, si contiene más puntos rojos que azules, entonces lo contrario será cierto. Dado que hay más puntos rojos que azules en cada hoja, el número total será clasificado correctamente con mayor frecuencia. Por tanto, el error se quedará estático o decrecerá.
Uno de los grandes problemas respecto a los algoritmos basados en árboles es que son bastante inconsistentes. Pequeñas diferencias en nuestros datos de entrenamiento pueden provocar árboles que se ven diametralmente diferentes. Por ende, cuando un árbol es usado para predecir datos que están ligeramente fuera del alcance de los datos usados para entrenarse dará malos resultados y produce variables con alta aleatoriedad.
Veamos los siguientes árboles que fueron entrenados con data sets similares y que tuvieron un buen desempeño con los datos en la esquina inferior izquierda. Al mismo tiempo, podemos ver que tuvieron resultados diferentes para el punto en azul. El problema aquí es la varianza que comúnmente afecta a los árboles.
Una técninca efectiva para reducir la varianza de un modelo es pasar de usar un simple árbol a usar una multitud de ellos. Con el gran poder de cómputo actual, no necesitamos limitarnos a un solo árbol. Fácilmente podemos generar cientos de ellos de golpe para sacar un promedio que nos dé un resultado final. Al sacar un promedio de tantos árboles, podemos garantizar que desaparezca cualquier anormalidad en cualquiera de los árboles.
A este método lo conocemos como Agregación de Bootstrap, aunque comúnmente se le llama Bagging. Esta es una de las formas de potenciar los árboles de decisión. Una desventaja de este enfoque, sin embargo, es que pierde interpretabilidad en comparación a un árbol clásico dado que ya no tenemos una cadena de decisiones clara.
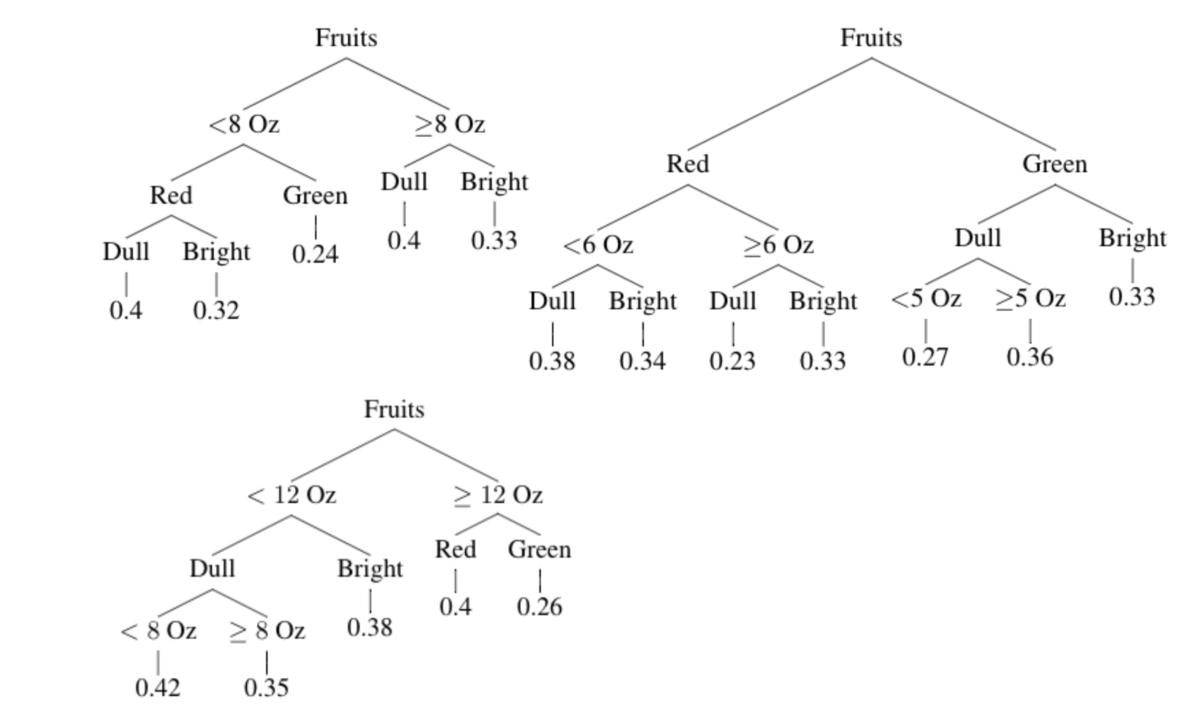
Veamos el siguente ejemplo:
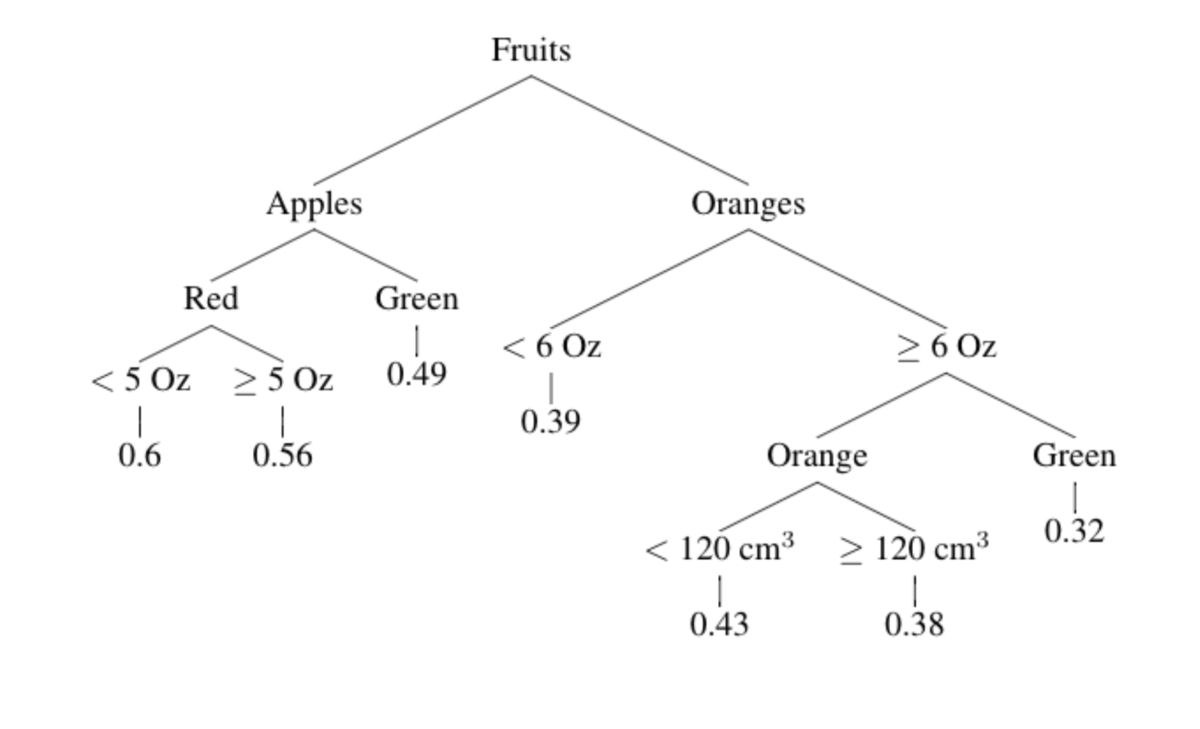
Si queremos tomar una decisión sobre la dulzura promedio de manzana roja simple que pese más de 6 onzas, sabemos que (siguiendo los árboles) el resultado es 0,35. Al seguir los caminos, podemos obtener las siguientes variables:
Peso < 8 -> roja -> simple: 0.4
Roja -> peso > 6 -> simple: 0.23
Peso < 12 -> simple -> peso < 8 -> 0.42
Dulzura = 0.4 + 0.23 + 0.42 / 3
= 0.35
Para generar todos los árboles, debemos de empezar con nuestros datos de entrenamiento. Ordinalmente, deberíamos usar cada punto de entrenamiento para generar un solo modelo. En este caso, empero, debemos generar varios por lo que necesitamos un enfoque diferente. Esencialmente, necesitamos obtener un dataset nuevo para cada árbol adicional que sea similar a nuestros datos de entrenamiento y al mismo tiempo únicos. De tal forma que generamos un árbol que se ajusta a nuestros datos pero que es único.
Al hacer bagging, el subconjunto de data points es creado con un sampleo aleatorio de nuestro data set completo. Si el data set completo contiene N puntos, entonces tomaremos N cantidad de muestras. El sampleo se hace con reemplazos, para que sea psoible para el subconjunto recibir el mismo punto varias veces. Posteriormente, entrenamos todos los sets necesarios y generamos todos los árboles con el mismo algoritmo. Finalmente, se dividen recursivamente las hojas para minimizar métricas.
Por ejemplo, si queremos usar un árbol de regresión lineal para predicir las alturas de las personas. Sería una pésima idea dividir muestras por sus pesos (digamos quienes pesan menos de 70 kgs y los que pesan más) ya que generaríamos un promedio que no representa al conjunto de datos.
Aunque parece que el bagging solo nos sirve para regresiones lineales, también podemos utilizarlo para clasificaciones. En este caso, cada árbol da un voto al predecir y la clasificación se da por el conteo de varios votos dados por varios árboles.
Supongamos que 7 árboles dan estos resultados al querer clasificar animales:
[Pato Ganso Pato Pichón Ganso Ganso Pichón]
El resultado en este caso sería Ganso porque es el punto que más se repite en el conjunto.
Por lo general, bagging es más efectivo si los árboles son diferentes. Esto tiene sentido porque si los árboles son muy similares, entonces harán errores similares y al promediar estos errores se verán reflejados. Para amortiguar esto, los árboles deben ser lo más diversos que se pueda.
El bagging puede ser mejorado asegurándonos que los árboles crezcan diferentemente, incluso si usamos data sets similares. Esta mejora es conocida como un random forest y complejiza un poco este algoritmo. Al igual que el bagging, un random forest genera arbitrariamente un número de arranque que usa para crear cada árbol. Sin embargo, el algoritmo de generación de árboles es algo "artificial". Si hay un número predictor de variables p, entonces el algoritmo del random forest será inicializar cuando m < p.
Al hacer una nueva decisión, el predictor m se elige arbitrariamente del set p y solo lo divide entre las variables consideradas. Como resultado, no hay variable que domine la construcción de árboles y eso generará el promedio de árboles.
Una alternativa al bagging es diseñar deliberadamente los árboles y que se complementan para cubrir las deficiencias de los otros. Es decir, no solo creamos árboles que se ajustan a los puntos originales sino a los errores de estos. A esto lo conocemos como Boosting.
Para esto, los árboles son incializados con los valores -B, d y λ, el número de árboles deseados, el número de divisiones en cada árbol y los pesos de cada árbol. Aquí asumimos que tenemos un gran data set con un número n de muestras de entrenamiento x1, x2, ... xn y un set correspondiente de variables de respuesta y1, y2, yn.
Finalmente, tenemos que inicializar f como f(x) = 0.
Por 1 ≤ b ≤ B:
- Creamos un conjunto de residuales r1, r2,... rn con ri = yi - *f(xi).
- Ajustamos el árbol f^b a los residuales, parando después de un número d de separaciones. Ajustamos f a f = f + λ f^b.
La función resultante sería:
A continuación dibujamos el primer ábol fb para generar el proceso de boosting. En el gŕafico describimos el data set que hemos generado de él, con la variable predictora representada por el eje x y el resultado representado en el eje y.
Empezamos nuestra función predictiva que es cero en todas partes. Basado en el primer árbol, nuestra nueva función predictora es:
f(x) = 0 + λf^b(x)
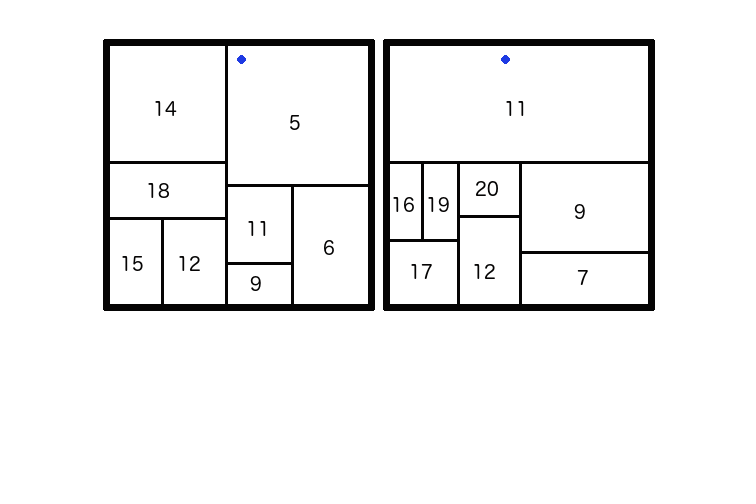
Si λ = 0.1 y siendo que el residual es el valor del punto que es usado en el árbol próximo ¿cual sería el residual del punto azul?
Para encontrar el residual del punto azul, debemos encontrar la predicción hecha por el primer árbol y luego sustraer esto del valor del punto azul después de pesarlo con λ.
Aquí, la estimación del árbol es 15 por lo que el valor de la función de la primera predicción en el punto azul es 0 + 0.1 ⋅ 15 = 1.5. Al sustraerlo el valor del punto azul da 13.5 para el residual ya que:
15 - 1.5 = 13.5
La función del algoritmo de boosting es el resultado de la suma de muchos errores, cada uno teniendo un peso por alguna constante λ. El valor de λ va de 0 a 1 y representa que tanta influencia un simple árbol debería de tener en el estimado final del modelo. Si es muy pequeño, la predicción de un solo árbol f^b(x) tendrá poco impacto en el resultado final.
Si tenemos que λ decrece, podemos entonces saber que el número B de árboles incrementa porque el resultado de cada árbol se multiplica por λ y después se añade al total de cada predicción. Por tanto y si λ es extremadamente pequeño, muchos árboles serán necesitados para alcanzar los número que queremos para predecir.
Con todo esto podríamos asumir que los algoritmos de boosting tienen una SEC menor al compararse con bagging. Sin embargo y en etapas tempranas, el boosting se desempeñará peor que el bagging porque la suma de los pesos de los árboles es mucho menor que los valores estimados. Esto es especialmente cierto si λ es un número menor y la SEC será mayor en etapas tempranas.
Aunque puede ser tentador utilizar boosting como una bala de plata, también tenemos que tener el sobreajuste en cuenta. Si tenemos un data set con números erroneos, es importante entonces tener un modelo que se resista a ser sobreajustado. Si se moldea demasiado a los datos que tenemos a la mano, dará mucho peso a valores que están obviamente equivocados.
Por tanto, el mejor modelo para este tipo de situaciones es bagging. Y aunque Boosting tiende a sobreajustarse rápidamente, es capaz de ajustarse bien a medida que tenemos más árboles. En comparación, bagging no escala tanto y su desempeño no mejorará a medida que incrementemos más árboles.
En el caso de las clasificaciones, el proceso es algo similar. Al iniciar el proceso, a cada data point se le da un peso que es una medida de cuan importante es para el árbol que estamos construyendo. A medida que construimos el árbol, los puntos que están siendo clasificados incorrectamente se les dan pesos grandes para enfocarse en ellos aún más.
Finalmente, todos los árboles votan en la clase de los puntos nuevos de la misma manera que en bagging. En el siguiente ejemplo enseñados datos usados para entrenar el primero y segundo árbol en el algoritmo de boosting. Además, se enseñan las lineas divisorias en cada uno de los pasos. Hay dos clases de puntos (rojo y azul) y el tamaño de un punto indica su importancia en un el árbol en donde se está construyendo.
Una de las grandes ventajas de los árboles de decisión es que son muy visuales en comparación con otros algoritmos de Machine Learning. Esto hace que sean fácil de interpretar. Y aunque los árboles de decisiones no suelen ser los más precisos al hacer predicciones, nos ayuda a encontrar interacciones entre variables dados su nivles de importancia.
Además, un árbol de decisión funciona bien para casí cualquier problema. Rara vez suele ser la mejor solución, pero se puede usar para casi cualquier problema.
Otra ventaja es que suele ser una buena solución cuando estamos trabajando con variables cualitativas. Muchos otros algoritmos tienen que ajustarse para lidiar con estos problemas. Mientras tanto, los árboles de decisiones puede trabajar directamente con este tipo de problemas. Con esto podemos evitar hacer suposiciones problemáticas que afecten nuestro modelado como asumir que puede haber un valor numérico que describa diferentes clases.
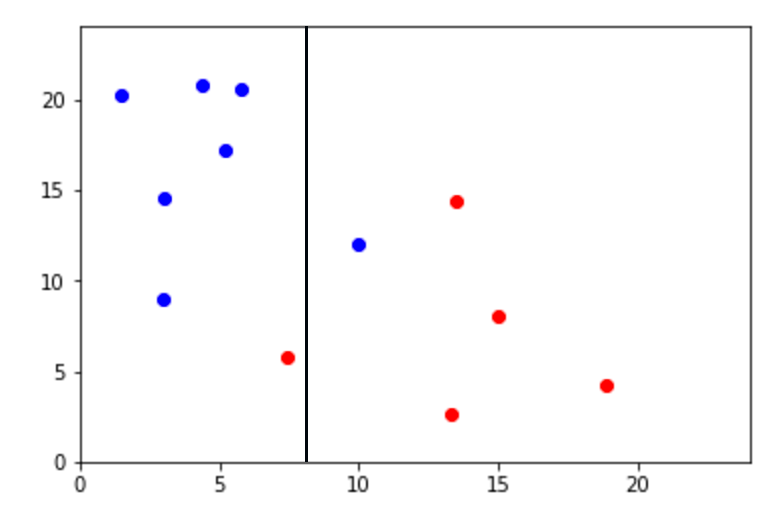
Sin embargo y aunque su interpretación es sencilla, existen limitaciones obvias a la hora de utilizar este enfoque. Rara vez podemos encontrar un fenómeno que pueda ser definido en bloques. Es por esta razón que los árboles de decisión no son la mejor opción para hacer predicciones. Un ejemplo es la siguiente imagen en la que es obvio que tenemos dos clases que pueden ser sencillamente divididos por una función linear. Sin embargo, un árbol de decisión tendría muchos problemas para este tipo de tareas.
Siempre que usemos árboles de decisión, tenemos que recordar que su desempeño con la data de entrenamiento no necesariamente refleja a los datos de la vida real. En especial porque los árboles son especialmente susceptibles a sufrir de sobreajustes. Es por esta razón que para este tipo de algoritmos solemos dividir la data en entrenamiento y pruebas. Los datos de entrenamiento sirven justo para lo que su nombre sugiere y con los de prueba evaluamos su desempeño. Debido a que estos son datos que el modelo no ha procesado, podemos saber que también es nuestro árbol de decisiones.