参与本项目,贡献其他语言版本的代码,拥抱开源,让更多学习算法的小伙伴们受益!
题目难度:中等
有一堆石头,每块石头的重量都是正整数。
每一回合,从中选出任意两块石头,然后将它们一起粉碎。假设石头的重量分别为 x 和 y,且 x <= y。那么粉碎的可能结果如下:
如果 x == y,那么两块石头都会被完全粉碎;
如果 x != y,那么重量为 x 的石头将会完全粉碎,而重量为 y 的石头新重量为 y-x。
最后,最多只会剩下一块石头。返回此石头最小的可能重量。如果没有石头剩下,就返回 0。
示例:
- 输入:[2,7,4,1,8,1]
- 输出:1
解释:
- 组合 2 和 4,得到 2,所以数组转化为 [2,7,1,8,1],
- 组合 7 和 8,得到 1,所以数组转化为 [2,1,1,1],
- 组合 2 和 1,得到 1,所以数组转化为 [1,1,1],
- 组合 1 和 1,得到 0,所以数组转化为 [1],这就是最优值。
提示:
- 1 <= stones.length <= 30
- 1 <= stones[i] <= 1000
《代码随想录》算法视频公开课:这个背包最多能装多少?LeetCode:1049.最后一块石头的重量II,相信结合视频再看本篇题解,更有助于大家对本题的理解。
如果对背包问题不熟悉的话先看这两篇:
本题其实是尽量让石头分成重量相同的两堆(尽可能相同),相撞之后剩下的石头就是最小的。
一堆的石头重量是sum,那么我们就尽可能拼成 重量为 sum / 2 的石头堆。 这样剩下的石头堆也是 尽可能接近 sum/2 的重量。 那么此时问题就是有一堆石头,每个石头都有自己的重量,是否可以 装满 最大重量为 sum / 2的背包。
看到这里,大家是否感觉和昨天讲解的 416. 分割等和子集非常像了,简直就是同一道题。
本题这样就化解成01背包问题了。
416. 分割等和子集 是求背包是否正好装满,而本题是求背包最多能装多少。
物品就是石头,物品的重量为stones[i],物品的价值也为stones[i]。
接下来进行动规五步曲:
dp[j]表示容量(这里说容量更形象,其实就是重量)为j的背包,最多可以背最大重量为dp[j]。
相对于 01背包,本题中,石头的重量是 stones[i],石头的价值也是 stones[i] 。
“最多可以装的价值为 dp[j]” 等同于 “最多可以背的重量为dp[j]”
01背包的递推公式为:dp[j] = max(dp[j], dp[j - weight[i]] + value[i]);
本题则是:dp[j] = max(dp[j], dp[j - stones[i]] + stones[i]);
既然 dp[j]中的j表示容量,那么最大容量(重量)是多少呢,就是所有石头的重量和。
因为提示中给出1 <= stones.length <= 30,1 <= stones[i] <= 1000,所以最大重量就是30 * 1000 。
而我们要求的target其实只是最大重量的一半,所以dp数组开到15000大小就可以了。
当然也可以把石头遍历一遍,计算出石头总重量 然后除2,得到dp数组的大小。
我这里就直接用15000了。
接下来就是如何初始化dp[j]呢,因为重量都不会是负数,所以dp[j]都初始化为0就可以了,这样在递归公式dp[j] = max(dp[j], dp[j - stones[i]] + stones[i]);中dp[j]才不会初始值所覆盖。
代码为:
vector<int> dp(15001, 0);
在动态规划:关于01背包问题,你该了解这些!(滚动数组)中就已经说明:如果使用一维dp数组,物品遍历的for循环放在外层,遍历背包的for循环放在内层,且内层for循环倒序遍历!
代码如下:
for (int i = 0; i < stones.size(); i++) { // 遍历物品
for (int j = target; j >= stones[i]; j--) { // 遍历背包
dp[j] = max(dp[j], dp[j - stones[i]] + stones[i]);
}
}
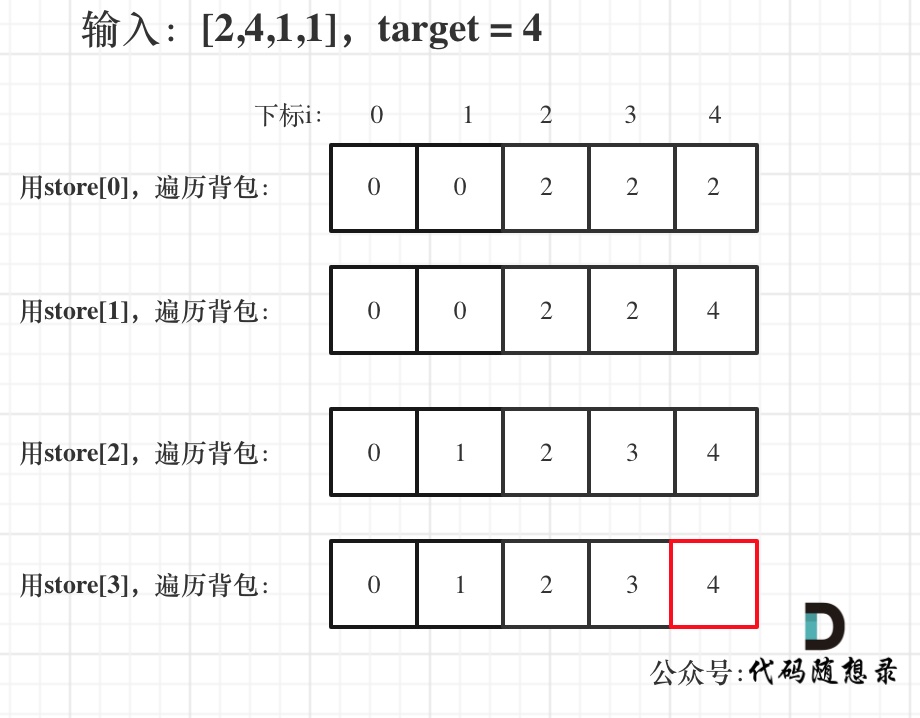
举例,输入:[2,4,1,1],此时target = (2 + 4 + 1 + 1)/2 = 4 ,dp数组状态图如下:
最后dp[target]里是容量为target的背包所能背的最大重量。
那么分成两堆石头,一堆石头的总重量是dp[target],另一堆就是sum - dp[target]。
在计算target的时候,target = sum / 2 因为是向下取整,所以sum - dp[target] 一定是大于等于dp[target]的。
那么相撞之后剩下的最小石头重量就是 (sum - dp[target]) - dp[target]。
以上分析完毕,C++代码如下:
class Solution {
public:
int lastStoneWeightII(vector<int>& stones) {
vector<int> dp(15001, 0);
int sum = 0;
for (int i = 0; i < stones.size(); i++) sum += stones[i];
int target = sum / 2;
for (int i = 0; i < stones.size(); i++) { // 遍历物品
for (int j = target; j >= stones[i]; j--) { // 遍历背包
dp[j] = max(dp[j], dp[j - stones[i]] + stones[i]);
}
}
return sum - dp[target] - dp[target];
}
};
- 时间复杂度:O(m × n) , m是石头总重量(准确的说是总重量的一半),n为石头块数
- 空间复杂度:O(m)
本题其实和416. 分割等和子集几乎是一样的,只是最后对dp[target]的处理方式不同。
416. 分割等和子集相当于是求背包是否正好装满,而本题是求背包最多能装多少。
一维数组版本
class Solution {
public int lastStoneWeightII(int[] stones) {
int sum = 0;
for (int i : stones) {
sum += i;
}
int target = sum >> 1;
//初始化dp数组
int[] dp = new int[target + 1];
for (int i = 0; i < stones.length; i++) {
//采用倒序
for (int j = target; j >= stones[i]; j--) {
//两种情况,要么放,要么不放
dp[j] = Math.max(dp[j], dp[j - stones[i]] + stones[i]);
}
}
return sum - 2 * dp[target];
}
}二维数组版本(便于理解)
class Solution {
public int lastStoneWeightII(int[] stones) {
int sum = 0;
for (int s : stones) {
sum += s;
}
int target = sum / 2;
//初始化,dp[i][j]为可以放0-i物品,背包容量为j的情况下背包中的最大价值
int[][] dp = new int[stones.length][target + 1];
//dp[i][0]默认初始化为0
//dp[0][j]取决于stones[0]
for (int j = stones[0]; j <= target; j++) {
dp[0][j] = stones[0];
}
for (int i = 1; i < stones.length; i++) {
for (int j = 1; j <= target; j++) {//注意是等于
if (j >= stones[i]) {
//不放:dp[i - 1][j] 放:dp[i - 1][j - stones[i]] + stones[i]
dp[i][j] = Math.max(dp[i - 1][j], dp[i - 1][j - stones[i]] + stones[i]);
} else {
dp[i][j] = dp[i - 1][j];
}
}
}
System.out.println(dp[stones.length - 1][target]);
return (sum - dp[stones.length - 1][target]) - dp[stones.length - 1][target];
}
}卡哥版
class Solution:
def lastStoneWeightII(self, stones: List[int]) -> int:
dp = [0] * 15001
total_sum = sum(stones)
target = total_sum // 2
for stone in stones: # 遍历物品
for j in range(target, stone - 1, -1): # 遍历背包
dp[j] = max(dp[j], dp[j - stone] + stone)
return total_sum - dp[target] - dp[target]卡哥版(简化版)
class Solution:
def lastStoneWeightII(self, stones):
total_sum = sum(stones)
target = total_sum // 2
dp = [0] * (target + 1)
for stone in stones:
for j in range(target, stone - 1, -1):
dp[j] = max(dp[j], dp[j - stone] + stone)
return total_sum - 2* dp[-1]
二维DP版
class Solution:
def lastStoneWeightII(self, stones: List[int]) -> int:
total_sum = sum(stones)
target = total_sum // 2
# 创建二维dp数组,行数为石头的数量加1,列数为target加1
# dp[i][j]表示前i个石头能否组成总重量为j
dp = [[False] * (target + 1) for _ in range(len(stones) + 1)]
# 初始化第一列,表示总重量为0时,前i个石头都能组成
for i in range(len(stones) + 1):
dp[i][0] = True
for i in range(1, len(stones) + 1):
for j in range(1, target + 1):
# 如果当前石头重量大于当前目标重量j,则无法选择该石头
if stones[i - 1] > j:
dp[i][j] = dp[i - 1][j]
else:
# 可选择该石头或不选择该石头
dp[i][j] = dp[i - 1][j] or dp[i - 1][j - stones[i - 1]]
# 找到最大的重量i,使得dp[len(stones)][i]为True
# 返回总重量减去两倍的最接近总重量一半的重量
for i in range(target, -1, -1):
if dp[len(stones)][i]:
return total_sum - 2 * i
return 0
一维DP版
class Solution:
def lastStoneWeightII(self, stones):
total_sum = sum(stones)
target = total_sum // 2
dp = [False] * (target + 1)
dp[0] = True
for stone in stones:
for j in range(target, stone - 1, -1):
# 判断当前重量是否可以通过选择之前的石头得到或选择当前石头和之前的石头得到
dp[j] = dp[j] or dp[j - stone]
for i in range(target, -1, -1):
if dp[i]:
# 返回剩余石头的重量,即总重量减去两倍的最接近总重量一半的重量
return total_sum - 2 * i
return 0
一维dp
func lastStoneWeightII(stones []int) int {
// 15001 = 30 * 1000 /2 +1
dp := make([]int, 15001)
// 求target
sum := 0
for _, v := range stones {
sum += v
}
target := sum / 2
// 遍历顺序
for i := 0; i < len(stones); i++ {
for j := target; j >= stones[i]; j-- {
// 推导公式
dp[j] = max(dp[j], dp[j-stones[i]]+stones[i])
}
}
return sum - 2 * dp[target]
}
func max(a, b int) int {
if a > b {
return a
}
return b
}二维dp
func lastStoneWeightII(stones []int) int {
sum := 0
for _, val := range stones {
sum += val
}
target := sum / 2
dp := make([][]int, len(stones))
for i := range dp {
dp[i] = make([]int, target + 1)
}
for j := stones[0]; j <= target; j++ {
dp[0][j] = stones[0]
}
for i := 1; i < len(stones); i++ {
for j := 0; j <= target; j++ {
if stones[i] > j {
dp[i][j] = dp[i-1][j]
} else {
dp[i][j] = max(dp[i-1][j], dp[i-1][j-stones[i]] + stones[i])
}
}
}
return (sum - dp[len(stones)-1][target]) - dp[len(stones)-1][target]
}
func max(x, y int) int {
if x > y {
return x
}
return y
}/**
* @param {number[]} stones
* @return {number}
*/
var lastStoneWeightII = function (stones) {
let sum = stones.reduce((s, n) => s + n);
let dpLen = Math.floor(sum / 2);
let dp = new Array(dpLen + 1).fill(0);
for (let i = 0; i < stones.length; ++i) {
for (let j = dpLen; j >= stones[i]; --j) {
dp[j] = Math.max(dp[j], dp[j - stones[i]] + stones[i]);
}
}
return sum - dp[dpLen] - dp[dpLen];
};#define MAX(a, b) (((a) > (b)) ? (a) : (b))
int getSum(int *stones, int stoneSize) {
int sum = 0, i;
for (i = 0; i < stoneSize; ++i)
sum += stones[i];
return sum;
}
int lastStoneWeightII(int* stones, int stonesSize){
int sum = getSum(stones, stonesSize);
int target = sum / 2;
int i, j;
// 初始化dp数组
int *dp = (int*)malloc(sizeof(int) * (target + 1));
memset(dp, 0, sizeof(int) * (target + 1));
for (j = stones[0]; j <= target; ++j)
dp[j] = stones[0];
// 递推公式:dp[j] = max(dp[j], dp[j - stones[i]] + stones[i])
for (i = 1; i < stonesSize; ++i) {
for (j = target; j >= stones[i]; --j)
dp[j] = MAX(dp[j], dp[j - stones[i]] + stones[i]);
}
return sum - dp[target] - dp[target];
}function lastStoneWeightII(stones: number[]): number {
const sum: number = stones.reduce((a: number, b:number): number => a + b);
const target: number = Math.floor(sum / 2);
const n: number = stones.length;
// dp[j]表示容量(总数和)为j的背包所能装下的数(下标[0, i]之间任意取)的总和(<= 容量)的最大值
const dp: number[] = new Array(target + 1).fill(0);
for (let i: number = 0; i < n; i++ ) {
for (let j: number = target; j >= stones[i]; j--) {
dp[j] = Math.max(dp[j], dp[j - stones[i]] + stones[i]);
}
}
return sum - dp[target] - dp[target];
};滚动数组:
object Solution {
def lastStoneWeightII(stones: Array[Int]): Int = {
var sum = stones.sum
var half = sum / 2
var dp = new Array[Int](half + 1)
// 遍历
for (i <- 0 until stones.length; j <- half to stones(i) by -1) {
dp(j) = math.max(dp(j), dp(j - stones(i)) + stones(i))
}
sum - 2 * dp(half)
}
}二维数组:
object Solution {
def lastStoneWeightII(stones: Array[Int]): Int = {
var sum = stones.sum
var half = sum / 2
var dp = Array.ofDim[Int](stones.length, half + 1)
// 初始化
for (j <- stones(0) to half) dp(0)(j) = stones(0)
// 遍历
for (i <- 1 until stones.length; j <- 1 to half) {
if (j - stones(i) >= 0) dp(i)(j) = stones(i) + dp(i - 1)(j - stones(i))
dp(i)(j) = math.max(dp(i)(j), dp(i - 1)(j))
}
sum - 2 * dp(stones.length - 1)(half)
}
}impl Solution {
pub fn last_stone_weight_ii(stones: Vec<i32>) -> i32 {
let sum = stones.iter().sum::<i32>();
let target = sum as usize / 2;
let mut dp = vec![0; target + 1];
for s in stones {
for j in (s as usize..=target).rev() {
dp[j] = dp[j].max(dp[j - s as usize] + s);
}
}
sum - dp[target] * 2
}
}public class Solution
{
public int LastStoneWeightII(int[] stones)
{
int[] dp = new int[15001];
int sum = 0;
foreach (int stone in stones)
{
sum += stone;
}
int target = sum / 2;
for (int i = 0; i < stones.Length; i++)
{
for (int j = target; j >= stones[i]; j--)
{
dp[j] = Math.Max(dp[j], dp[j - stones[i]] + stones[i]);
}
}
return sum - 2 * dp[target];
}
}