Skip to content

Latest commit

 

History

History
651 lines (427 loc) · 17.4 KB

README.md

File metadata and controls

651 lines (427 loc) · 17.4 KB

Binary Trees Data-Structures and Algorithms

Note. The name of function which is same but _ before name is helper function.

01. Binary Trees: Traversal Algorithms Pre-order

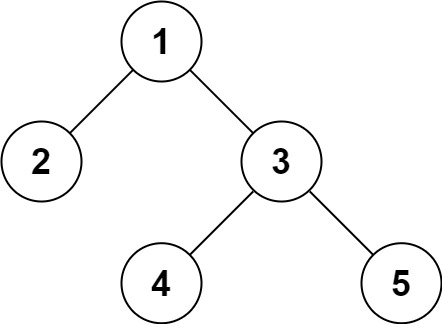
Binary Trees: Traversal Algorithms Pre-order

There are three recursive depth-first search traversal algorithms (preorder, inorder, and postorder) and implement those recursively in Python.

Pre-Order Traversal:

                1
            /       \
            2          3
          /   \       /  \
        4      5    6     7

This technique follows the 'root left right' policy. It means that, first root node is visited after that the left subtree is traversed recursively, and finally, right subtree is recursively traversed. As the root node is traversed before (or pre) the left and right subtree, it is called preorder traversal.

So, in a preorder traversal, each node is visited before both of its subtrees.

                          (root -> left -> right)

so, above preorder traversal output will be :
                                        1-2-4-5-3-6-7

02. Binary Trees: Traversal Algorithms In-order

Binary Trees: Traversal Algorithms In-order

There are three recursive depth-first search traversal algorithms (preorder, inorder, and postorder) and implement those recursively in Python.

In-Order Traversal:

            1
        /       \
        2          3
      /   \       /  \
    4      5    6     7

This technique follows the 'left root right' policy. It means that first left subtree is visited after that root node is traversed, and finally, the right subtree is traversed. As the root node is traversed between the left and right subtree, it is named inorder traversal.

So, in the inorder traversal, each node is visited in between of its subtrees.

                      (root -> left -> right)

so, above inorder traversal output will be :
                                    4-2-5-1-6-3-7-

03. Binary Trees: Traversal Algorithms Post-order

Binary Trees: Traversal Algorithms Post-order

There are three recursive depth-first search traversal algorithms (preorder, inorder, and postorder) and implement those recursively in Python.

Post-Order Traversal:

                1
            /       \
            2          3
          /   \       /  \
        4      5    6     7

This technique follows the 'left-right root' policy. It means that the first left subtree of the root node is traversed, after that recursively traverses the right subtree, and finally, the root node is traversed. As the root node is traversed after (or post) the left and right subtree, it is called postorder traversal.

So, in a postorder traversal, each node is visited after both of its subtrees.

                          (left -> right -> root)

so, above postorder traversal output will be :
                                        4-5-2-6-7-3-1-

04. Binary Trees: Traversal Algorithms Level-order

Binary Trees: Traversal Algorithms Level-order

Level-Order Traversal:

                1
            /     \
            2        3
          /  \
        4    5

Given a binary tree, the task is to print the level order traversal line by line of the tree

Level Order Traversal is the algorithm to process all nodes of a tree by traversing through depth, first the root, then the child of the root, etc.

In simple word level-order traversal will print the node according to level.

so, above level-order traversal output will be :
                                        1-2-3-4-5-

05. Binary Trees: Traversal Algorithms Reverse Level-order

Binary Trees: Traversal Algorithms Reverse Level-order

Level-Order Traversal:

                1
            /     \
            2        3
          /  \
        4    5

Given a binary tree, the task is to print the reverse level order traversal line by line of the tree

The idea is to print the last level first, then the second last level, and so on. Like Level order traversal, every level is printed from left to right.

so, above reverse level-order traversal output will be :
                                                        4-5-2-3-1-

06. Binary Trees: Calculating Height of Tree

Binary Trees: Calculating Height of Tree

It will return the height of the binary tree

                (1)
                  1
            (1)  /   \ (0)
                2      3
          (0)  /  \  (0)
              4     5

The height of leaf node with data 4 is 0 because there is no child node present
The height of leaf node with data 5 is 0 because there is no child node present
The height of leaf node with data 3 is 0 because there is no child node present

The height of node with data 2 is 1 becase the max between two child node + 1 is the height of node
example:
        1 + max(left_child, right_child)
        1 + max(0, 0)
        1 + 0
        1

The height of node with data 1 is 2 becase the max between two child node + 1 is the height of node
example:
        1 + max(left_child, right_child)
        1 + max(1, 0)
        1 + 1
        1

max will return the maximum number of given 2 numbers

so, the height of this binary tree is: 2

07. Binary Trees: Calculating Size of Tree

Binary Trees: Calculating Size of Tree

It will return the size of the binary tree

                  1
                /  \
                2     3
              /  \
              4     5

To calculate the size of the binary tree we use stack data structure to keep record of the nodes
by push and pop operations.

Example:
            start from root node

            1

            push onto stack

            stack : [1]

            make size 1

            pop from the stack and check if root node have childrens, so push childrens onto the stack.

            stack : [2, 3]

            size = 3

            pop one by one and check if popped node have any children, if yes push, otherwize make size ++

            stack : [4, 5, 3]

            size = 5

            stack : [5, 3]

            stack : [3]

            stack : []

so, the size of this binary tree is: 5

08. Binary Trees: Invert Binary Tree

Leetcode Problem URL

Given the root of a binary tree, invert the tree, and return its root.

Input :
                  4
                /   \
               2     7
              / \   / \
             1   3 6    9

Output :
                  4
                /   \
               7     2
              / \   / \
             9   6 3    1

Example 1:
Input: root = [4,2,7,1,3,6,9]
Output: [4,7,2,9,6,3,1]

Example 2:
Input: root = [2,1,3]
Output: [2,3,1]

Example 3:
Input: root = []
Output: []

09. Binary Trees: Maximum Depth of Binary Tree

Leetcode Problem URL

Given the root of a binary tree, return its maximum depth.

A binary tree's maximum depth is the number of nodes along the longest path from the root node down to the farthest leaf node.

Example 1:

                  3
                 / \
                9   20
                   /  \
                  15   7

Input: root = [3,9,20,null,null,15,7]
Output: 3

Example 2:
Input: root = [1,null,2]
Output: 2

10. Binary Trees: Subtree Of Another Tree

Leetcode Problem URL

Given the roots of two binary trees root and subRoot, return true if there is a subtree of root with the same structure and node values of subRoot and false otherwise.

A subtree of a binary tree tree is a tree that consists of a node in tree and all of this node's descendants. The tree tree could also be considered as a subtree of itself.

Example 1:

Alt text

Input: root = [3,4,5,1,2], subRoot = [4,1,2]
Output: true

Example 2:

Alt text

Input: root = [3,4,5,1,2,null,null,null,null,0], subRoot = [4,1,2]
Output: false

11. Binary Trees: Level Order Traversal - BFS

Leetcode Problem URL

Given the root of a binary tree, return the level order traversal of its nodes' values. (i.e., from left to right, level by level).

Example 1:

Alt text

Input: root = [3,9,20,null,null,15,7]
Output: [[3],[9,20],[15,7]]

Example 2:

Input: root = [1]
Output: [[1]]

Example 3:

Input: root = []
Output: []

12. Binary Trees: Construct Binary Tree from Preorder and Inorder Traversal

Leetcode Problem URL

Given two integer arrays preorder and inorder where preorder is the preorder traversal of a binary tree and inorder is the
inorder traversal of the same tree, construct and return the binary tree.

Example 1:

Alt text

Input: preorder = [3,9,20,15,7], inorder = [9,3,15,20,7]
Output: [3,9,20,null,null,15,7]

Example 2:

Input: preorder = [-1], inorder = [-1]
Output: [-1]

Example 3:

Input: root = []
Output: []

13. Binary Trees: Construct Binary Tree from Inorder and Postorder Traversal

Leetcode Problem URL

Given two integer arrays inorder and postorder where inorder is the inorder traversal of a binary tree and postorder
is the postorder traversal of the same tree, construct and return the binary tree.

Example 1:

Alt text

Input: inorder = [9,3,15,20,7], postorder = [9,15,7,20,3]
Output: [3,9,20,null,null,15,7]

Example 2:

Input: inorder = [-1], postorder = [-1]
Output: [-1]

14. Binary Trees: Maximum Path Sum

Leetcode Problem URL

A path in a binary tree is a sequence of nodes where each pair of adjacent nodes in the sequence has an edge connecting them.
A node can only appear in the sequence at most once. Note that the path does not need to pass through the root.

The path sum of a path is the sum of the node's values in the path.

Given the root of a binary tree, return the maximum path sum of any non-empty path.

Example 1:

Alt text

Input: root = [1,2,3]
Output: 6
Explanation: The optimal path is 2 -> 1 -> 3 with a path sum of 2 + 1 + 3 = 6.

Example 2:

Alt text

Input: root = [-10,9,20,null,null,15,7]
Output: 42
Explanation: The optimal path is 15 -> 20 -> 7 with a path sum of 15 + 20 + 7 = 42.

15. Binary Trees: Serialize and Deserialize

Leetcode Problem URL

Serialization is the process of converting a data structure or object into a sequence of bits so that it can be stored in a file or memory buffer, or transmitted across a network connection link to be reconstructed later in the same or another computer environment.

Design an algorithm to serialize and deserialize a binary tree. There is no restriction on how your serialization/deserialization algorithm should work. You just need to ensure that a binary tree can be serialized to a string and this string can be deserialized to the original tree structure.

Clarification: The input/output format is the same as how LeetCode serializes a binary tree. You do not necessarily need to follow this format, so please be creative and come up with different approaches yourself.

As stated explicitly in the clarification above, I can also come up with alternative approaches, therefore I implemented this problem with depth first search (preorder) traversal.

Example 1:

Alt text

Input: root = [1,2,Null,Null,3,4,Null,Null,5,Null,Null]
Output: Serialized: 1,2,Null,Null,3,4,Null,Null,5,Null,Null
        Deserialized: 1,2,Null,Null,3,4,Null,Null,5,Null,Null

Explanation

Here is a step-by-step Explanation of how the implemented code works using the first input nums1 = [1, 2, None, None, 3, 4, None, None, 5, None, None].

1. Building the Binary Tree

  • Input: nums1 = [1, 2, None, None, 3, 4, None, None, 5, None, None]
  • Function: buildBT(nums)
  • Purpose: Construct a binary tree using preorder traversal from the given list.

The buildBT function defines a helper function build that recursively constructs the tree in a preorder manner.

Construction Steps:

  1. Start with index = 0, which corresponds to the root node value 1.

    • Create a TreeNode with value 1.
    • Recursively build the left subtree starting from index = 1.

  2. At index = 1, value is 2.

    • Create a TreeNode with value 2.
    • Recursively build the left subtree starting from index = 2.

  3. At index = 2, value is None.

    • Return None and move to index = 3.

  4. At index = 3, value is None.

    • Return None and move to index = 4.
    • The left subtree of node 2 is None and the right subtree is None.

  5. Back to node 1, recursively build the right subtree starting from index = 4.

  6. At index = 4, value is 3.

    • Create a TreeNode with value 3.
    • Recursively build the left subtree starting from index = 5.

  7. At index = 5, value is 4.

    • Create a TreeNode with value 4.
    • Recursively build the left subtree starting from index = 6.

  8. At index = 6, value is None.

    • Return None and move to index = 7.

  9. At index = 7, value is None.

    • Return None and move to index = 8.
    • The left subtree of node 4 is None and the right subtree is None.

  10. Back to node 3, recursively build the right subtree starting from index = 8.

  11. At index = 8, value is 5.

    • Create a TreeNode with value 5.
    • Recursively build the left subtree starting from index = 9.

  12. At index = 9, value is None.

    • Return None and move to index = 10.

  13. At index = 10, value is None.

    • Return None and move to index = 11.
    • The left subtree of node 5 is None and the right subtree is None.

The constructed binary tree is:

    1
   / \
  2   3
     / \
    4   5

2. Serializing the Binary Tree

  • Function: serialize(self, root)
  • Purpose: Convert the binary tree into a string using preorder traversal.

Serialization Steps:

  1. Initialize an empty list res.
  2. Define a recursive helper function preorder_dfs(node) to perform preorder traversal.
  3. Traverse the tree and append node values to res:
    • Visit root node 1 and append "1".
    • Visit left child 2 and append "2".
    • Left and right children of 2 are None, append "Null" twice.
    • Visit right child 3 and append "3".
    • Visit left child 4 and append "4".
    • Left and right children of 4 are None, append "Null" twice.
    • Visit right child 5 and append "5".
    • Left and right children of 5 are None, append "Null" twice.
  4. Join res with commas to form the serialized string: "1,2,Null,Null,3,4,Null,Null,5,Null,Null".

3. Deserializing the String

  • Function: deserialize(self, data)
  • Purpose: Reconstruct the binary tree from the serialized string.

Deserialization Steps:

  1. Split the serialized string into a list vals.
  2. Initialize an index pointer self.i to 0.
  3. Define a recursive helper function preorder_dfs() to perform preorder reconstruction.
  4. Reconstruct the tree:
    • At self.i = 0, value is "1", create root node 1.
    • Increment self.i and reconstruct the left subtree.
      • At self.i = 1, value is "2", create left child node 2.
      • Increment self.i and reconstruct its left subtree.
        • At self.i = 2, value is "Null", return None.
      • Increment self.i and reconstruct its right subtree.
        • At self.i = 3, value is "Null", return None.
    • Increment self.i and reconstruct the right subtree.
      • At self.i = 4, value is "3", create right child node 3.
      • Increment self.i and reconstruct its left subtree.
        • At self.i = 5, value is "4", create left child node 4.
        • Increment self.i and reconstruct its left subtree.
          • At self.i = 6, value is "Null", return None.
        • Increment self.i and reconstruct its right subtree.
          • At self.i = 7, value is "Null", return None.
      • Increment self.i and reconstruct its right subtree.
        • At self.i = 8, value is "5", create right child node 5.
        • Increment self.i and reconstruct its left subtree.
          • At self.i = 9, value is "Null", return None.
        • Increment self.i and reconstruct its right subtree.
          • At self.i = 10, value is "Null", return None.

The reconstructed binary tree matches the original tree structure.

Verification

Finally, serialize the deserialized tree again to verify correctness:

  • Serialize the tree obtained from deserialization and check if it matches the original serialized string: "1,2,Null,Null,3,4,Null,Null,5,Null,Null".

The output confirms that the serialization and deserialization processes work as intended, accurately preserving the tree structure.

Example 2:

Input: root = []
Output: Serialized: Null
        Deserialized: Null